Chapter 5 Geometry

Section 5.6 Trigonometric Functions: Sine, et cetera

5.6.3 Trigonometry in the Unit Circle

In the previous section the trigonometric functions were introduced by means of a right triangle. Hence, the properties described above are valid for an angle ranging from $0{}^{\circ }$ to $90{}^{\circ }$ or from $0$ to $\frac{\pi }{2}$, respectively.
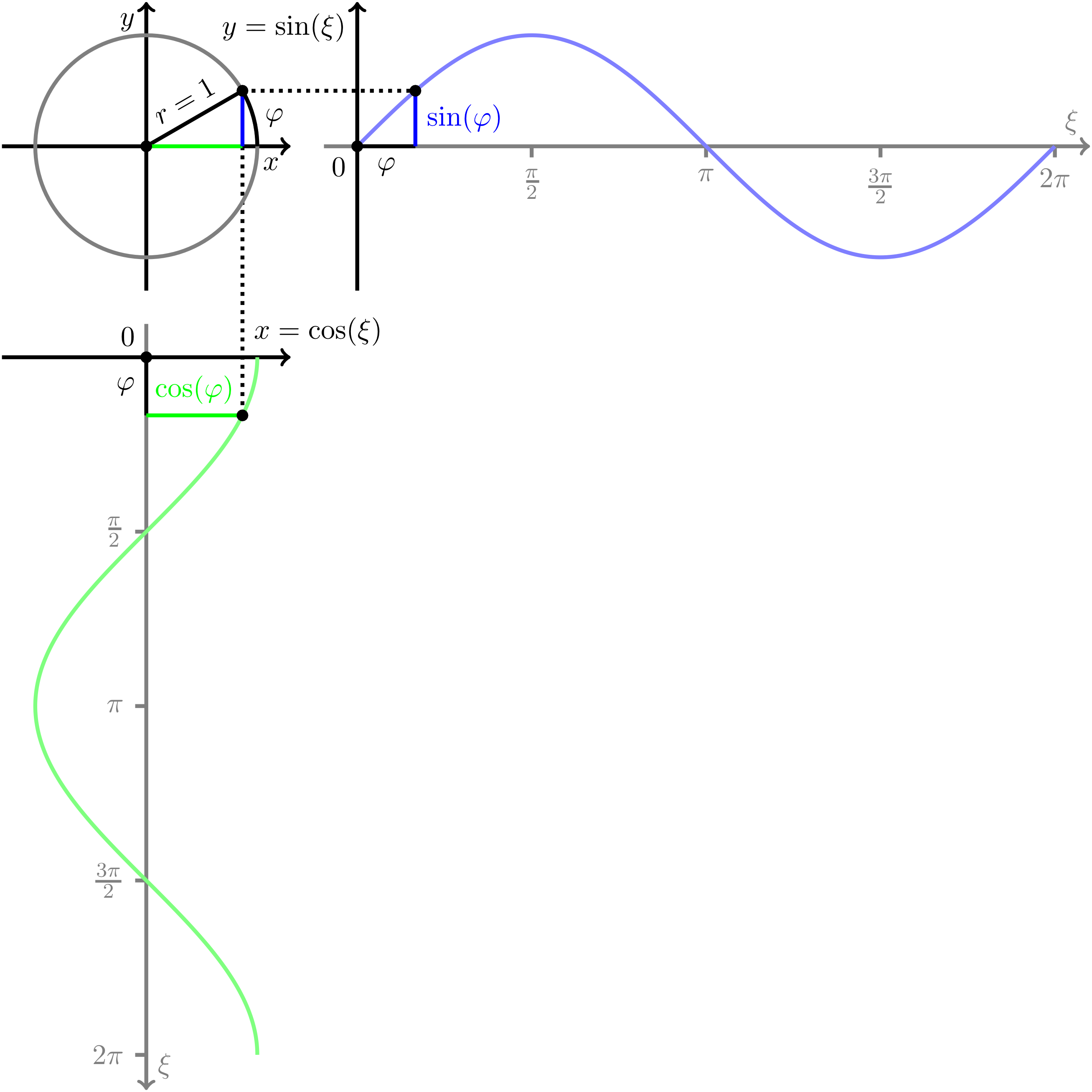
To extend the acquired insights to angles greater than $\pi /2$, it is particularly useful to investigate the so-called unit circle.

The unit circle is a circle with a radius of $1$. Its centre is positioned at the origin in the Cartesian coordinate system. Consider a line segment of length $1$ starting from the centre. From its horizontal initial position on the positive $x$-axis, this segment is now rotated counter-clockwise, i.e. in the mathematical positive direction, around its centre. In this process, its rotating end point is sweeping the unit circle enclosing the angle $\phi$ with the positive $x$-axis. During rotation, the angle $\phi$ increases from $0$ to $2\pi$ or $360{}^{\circ }$, respectively. Thus, to any angle $\phi$ there corresponds a point with the coordinates $x_{\phi }$ and $y_{\phi }$ on the unit circle.
For $\phi$ from $0$ to $\frac{\pi }{2}$, the line segment, the corresponding segment on the $x$-axis, and the the corresponding segment on the $y$-axis can be regarded as a right triangle. The hypotenuse is the line segment of length $1$, the $x$-intercept is the adjacent side, and the $y$-intercept is the opposite side. This matches the situation described in the previous section.
Hence, the sine of the angle $\phi$ is

${\displaystyle \sin \left(\phi \right)=\frac{y_{\phi }}{1}=y_{\phi }}$
and the cosine is

${\displaystyle \cos \left(\phi \right)=\frac{x_{\phi }}{1}=x_{\phi }\hspace{0.5em}.}$
Based on the description above, these definitions now are also valid for angles $\phi >\pi /2$. Here, the values of $x_{\phi }$ and $y_{\phi }$ can be negative as well, hence also sine and cosine can be negative. If the $y$-values are plotted against the angle $\phi$, one obtains for the sine function the blue curve. Plotting $y$-values against the angle $\phi$ one obtains for the cosine function the green curve. If the line segment is rotated in the opposite direction, values for negative angles can be defined accordingly.
Furthermore, using Pythagoras' theorem, we have

${\displaystyle x_{\phi }^2+y_{\phi }^2=1\hspace{0.5em}.}$
Replacing $x_{\phi }$ and $y_{\phi }$ by the corresponding relations to the trigonometric functions results for any $\phi$ in the important relation

${\displaystyle {\sin }^2\left(\phi \right)+{\cos }^2\left(\phi \right)=1\hspace{0.5em}.}$
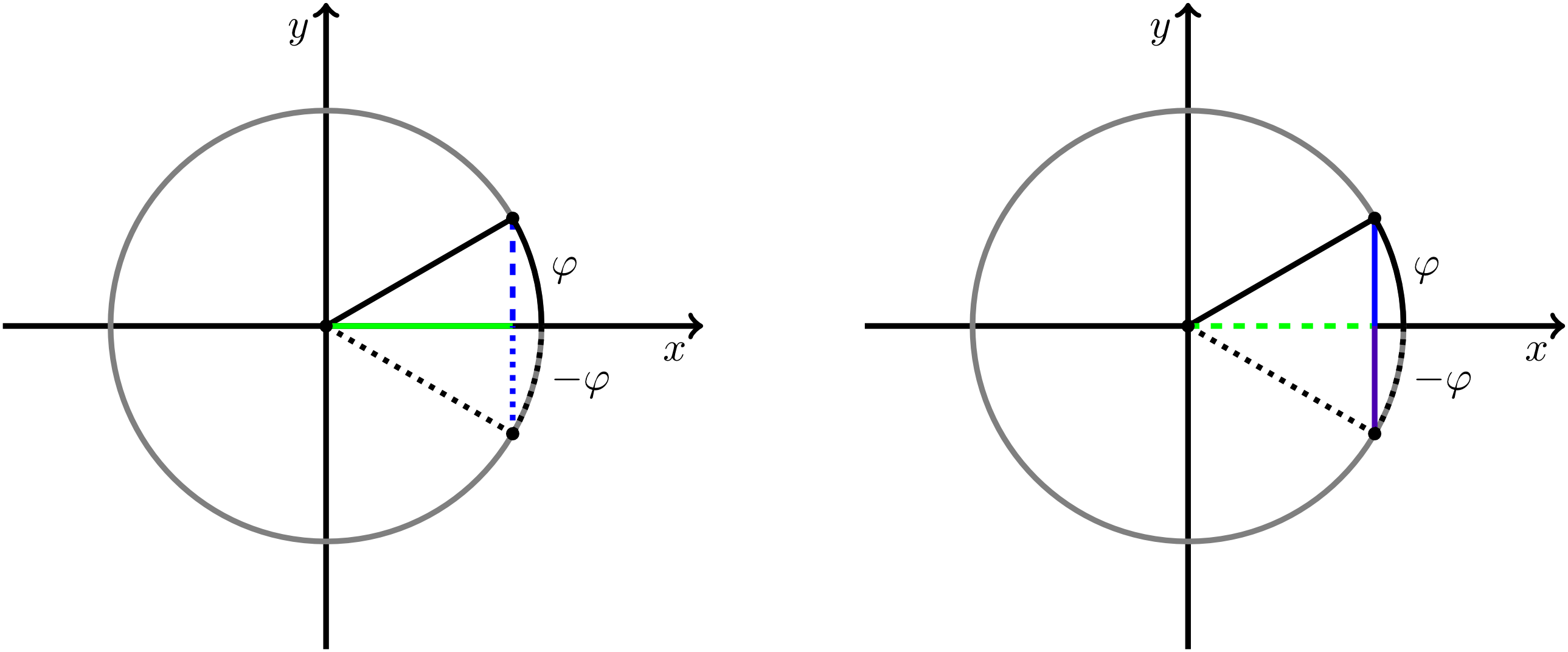
Additionally, from the description of the sine and cosine function, it can be seen that the values of the cosine function do not change if the line segment is reflected across the $x$-axis. Hence, the cosine value of the angle $\phi$ is equal to the cosine value of the angle $-\phi$ (indicated in the figure below by the green line). For the sine function, a reflection across the $x$-axis results in a change of sign of the sine value (indicated in the figure below by the blue line and the violet line, respectively)

Expressed in formulas, this is

${\displaystyle \cos (-\phi )=\cos (\phi )\mathrm{ }\text{and}\mathrm{ }\sin (-\phi )=-\sin (\phi )}$
for every angle $\phi$. These symmetry properties are useful for many calculations. An elementary example is the calculation of the angle between the $x$-axis and the connecting line from the origin to a point in the Cartesian coordinate system (see also Exercise 5.6.9).