Chapter 5 Geometry

Section 5.4 Polygons, Area and Circumference

5.4.4 Circumference

The circumference of a polygon is the sum of the lengths of all its line segments. If a polygon has further properties concerning the side lengths, more statements concerning the circumference can hold.
First, quadrilaterals are considered. If $a$ and $b$ are adjacent sides of a parallelogram, then its circumference is $U=a+b+a+b=2·a·b$.
For a rhombus (and therefore for a square), all four sides have the same length $a$ such that its circumference is $U=4·a$.
Likewise, for every regular polygon, all sides have the same length. If $n$ is the number of vertices and $a$ is the length of a side, then the circumference $U_n$ can simply be calculated by $U_n=n·a$.
As an outlook to trigonometric functions described in Section 5.6 the circumference of a regular polygon shall now be calculated in another way.

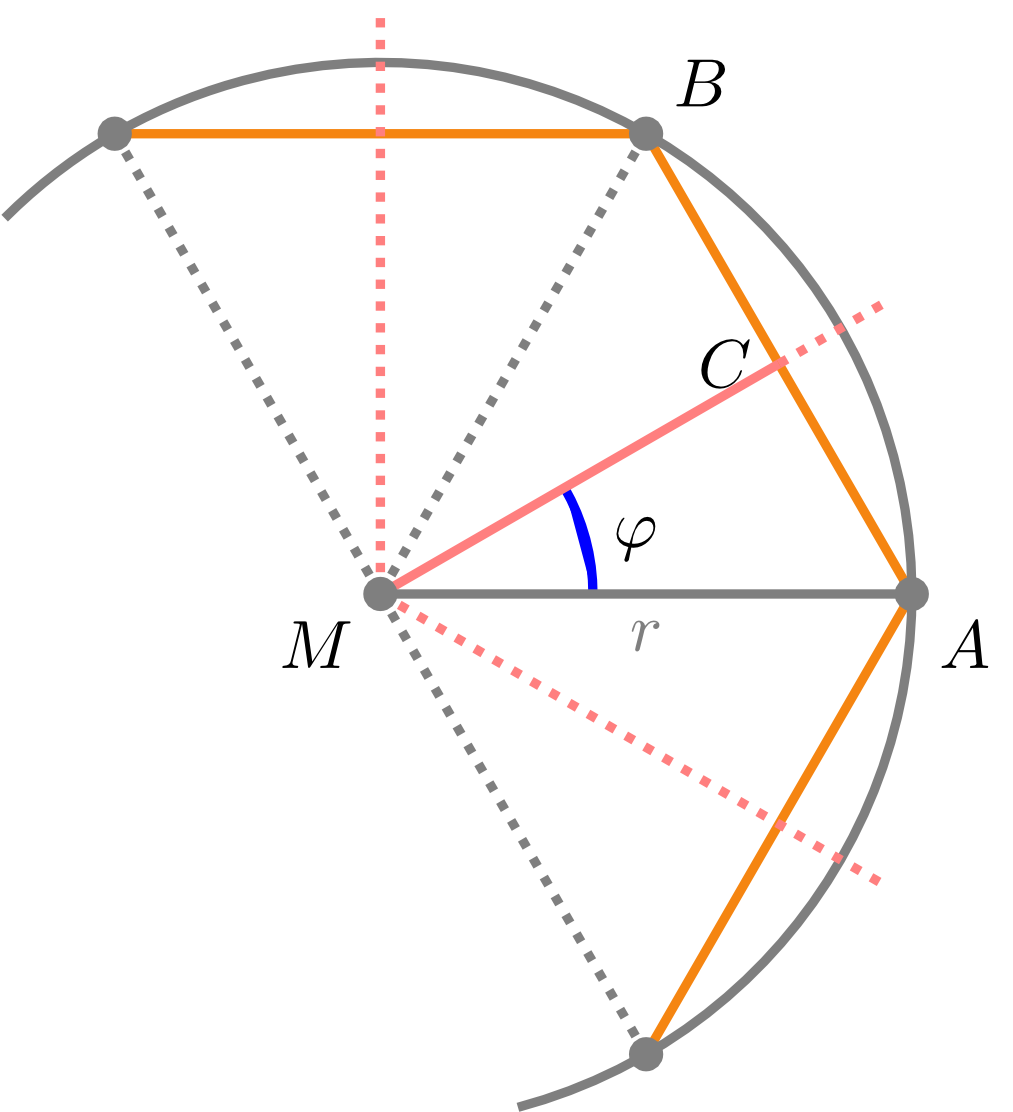
The vertices of a regular polygon all lie on a common circle with radius $r$. The angle $\phi$ between the line segments connecting the centre of the circle to the vertices $A$ and $B$ of a side is the $n$-th part of the complete angle: $\phi =\frac{2\pi }{n}$. The centre of the circle and the midpoint $C$ of the line segment $\overline{AB}$ form a right triangle $MAC$ with the angle $\measuredangle (\mathrm{AMC})=\frac{1}{2}·\phi =\frac{\pi }{n}$. If the value of $a$ is calculated by

${\displaystyle \sin (\measuredangle (\mathrm{AMC}))=\frac{\frac{1}{2}a}{r}}$
and is inserted in $U=n·a$, then we obtain the formula

${\displaystyle U_n=n·a=2·r·n·\sin \left(\frac{\pi }{n}\right)}$
for the circumference of a regular polygon. For example, $U_6=2·r·6·\frac{1}{2}=6·r$. The larger $n$ is, the closer the circumference is to the value $2·r·\pi \approx 6.283·r$ describing the circumference of a circle with radius $r$. This can be shown by means of more advanced methods of calculus, the basic ideas of which are introduced in Chapter 7. The approach described here is based on the following idea: it is difficult to calculate the value of the circumference of a circle. Therefore, one looks for similar objects, in this case the regular polygons, with two properties: their circumference can be calculated easily, and if the number of vertices is sufficiently large, then the circumference of the polygon differs from the circumference of a circle less than any given positive number (here, one thinks of "small" numbers). This approach can also be used to calculate the area of surfaces that are not bounded by line segments (see Chapter 8). For this purpose, it will be illustrated here how to calculate the area of polygons, which is in this respect relatively easy. Further, this can be used as the starting point of an approximation, as the figure above showing a circle inscribed into a hexagon suggests.