Chapter 5 Geometry
Section 5.2 Angles and Angle Measurement5.2.2 Angles
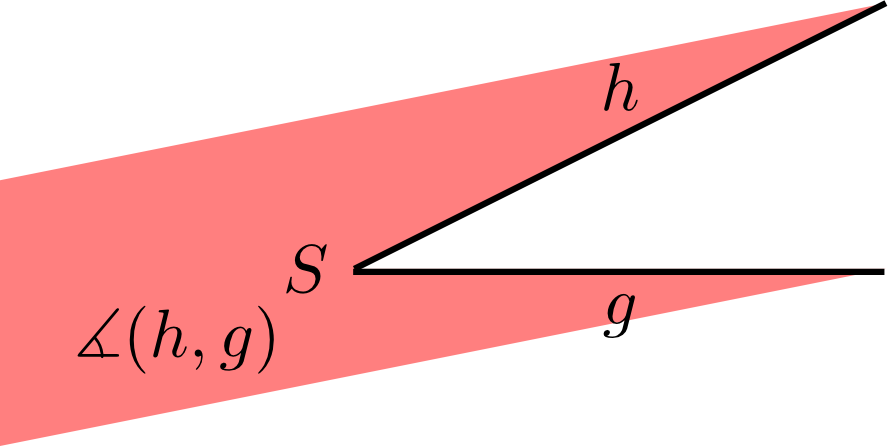
Two rays (half-lines) and in the plane starting from the same initial point enclose an angle .For the notation of the angle , the order of and is relevant. denotes the angle shown in the figure above. It is defined by rotating the half-line counter-clockwise to the half-line .
In contrast, denotes the angle from to as illustrated by the figure below.
The point is called a vertex of the angle, and the two half-lines enclosing the angle are called the arms of the angle. If is a point on the line and is a point on the line , then the angle can also be denoted by . In this way, angles between line segments and are described.
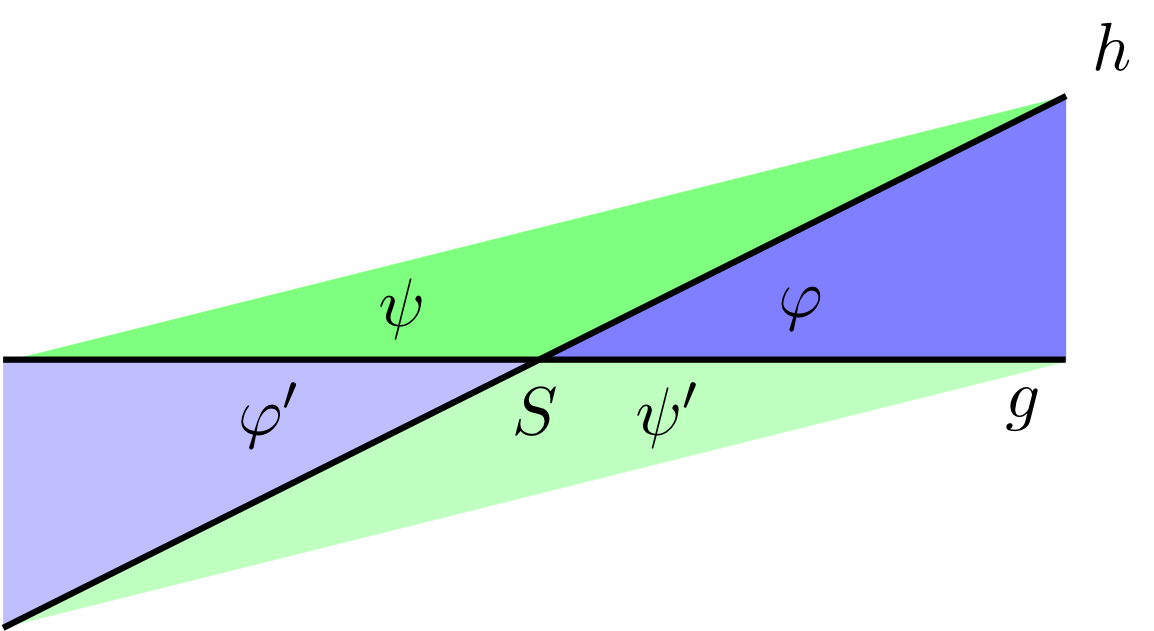
Angles are often denoted by lower-case Greek letters to distinguish them from variables, which are generally denoted by lower-case Latin letters (see Table 1.1.8 in module 1). Further angles can be found by considering angles formed by intersecting lines.
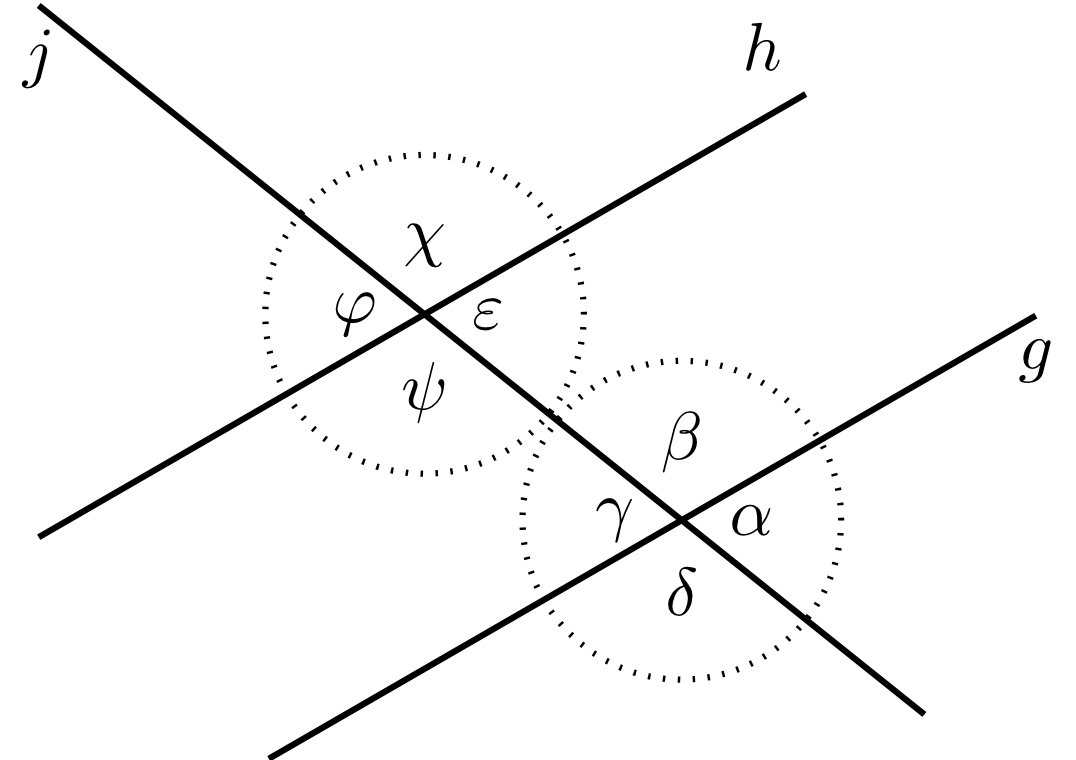
The figure above contains further vertical and supplementary angles.
Exercise 5.2.2
Find all vertical and supplementary angles occurring in the figure above.
Some special angles have their own dedicated name. For example, the angle bisector is the half-line whose points have the same distance from the two given half-lines and . Then, it can be said that bisects the angle between and .
Names of Special Angles 5.2.3
Let and be half-lines with the intersection point .
- The angle covering the entire plane is called the complete angle.
- If the rays and form a line, the angle between and is called a straight angle.
- The angle between two half-lines bisecting a straight angle is called the right angle. One also says that and are perpendicular (or orthogonal) to each other.
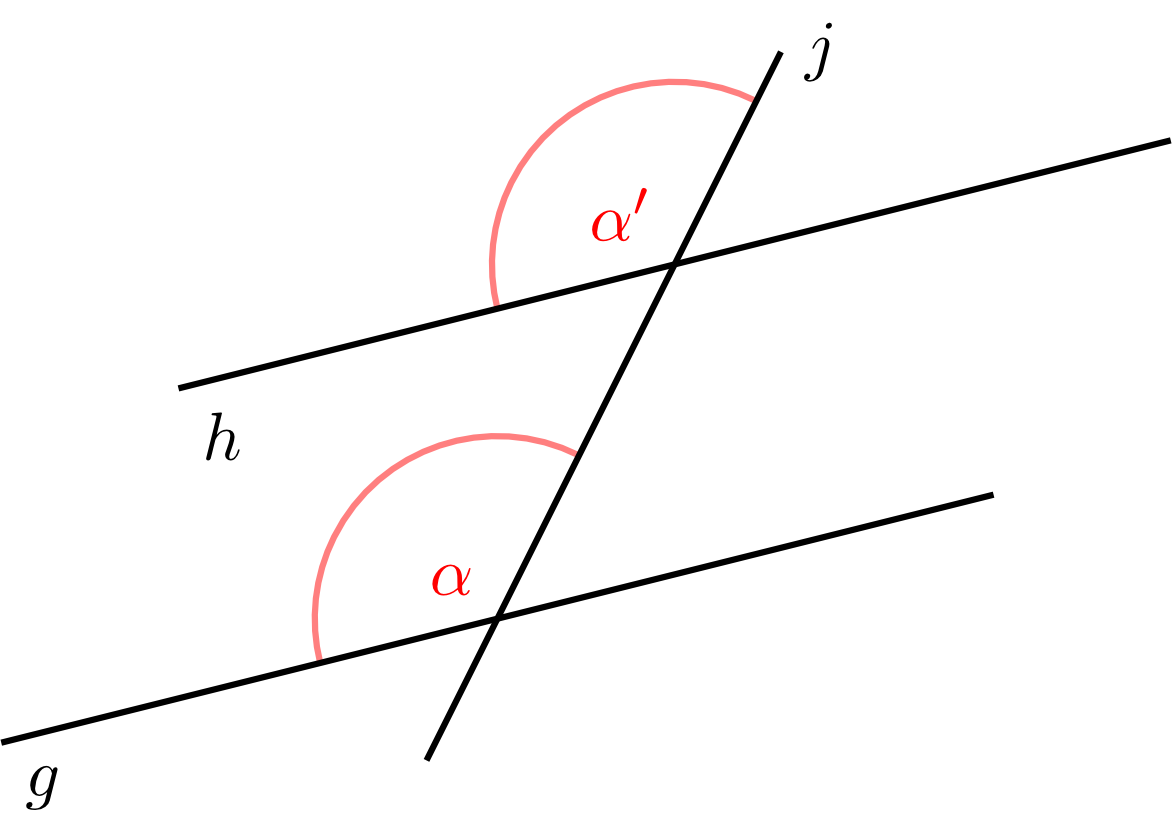
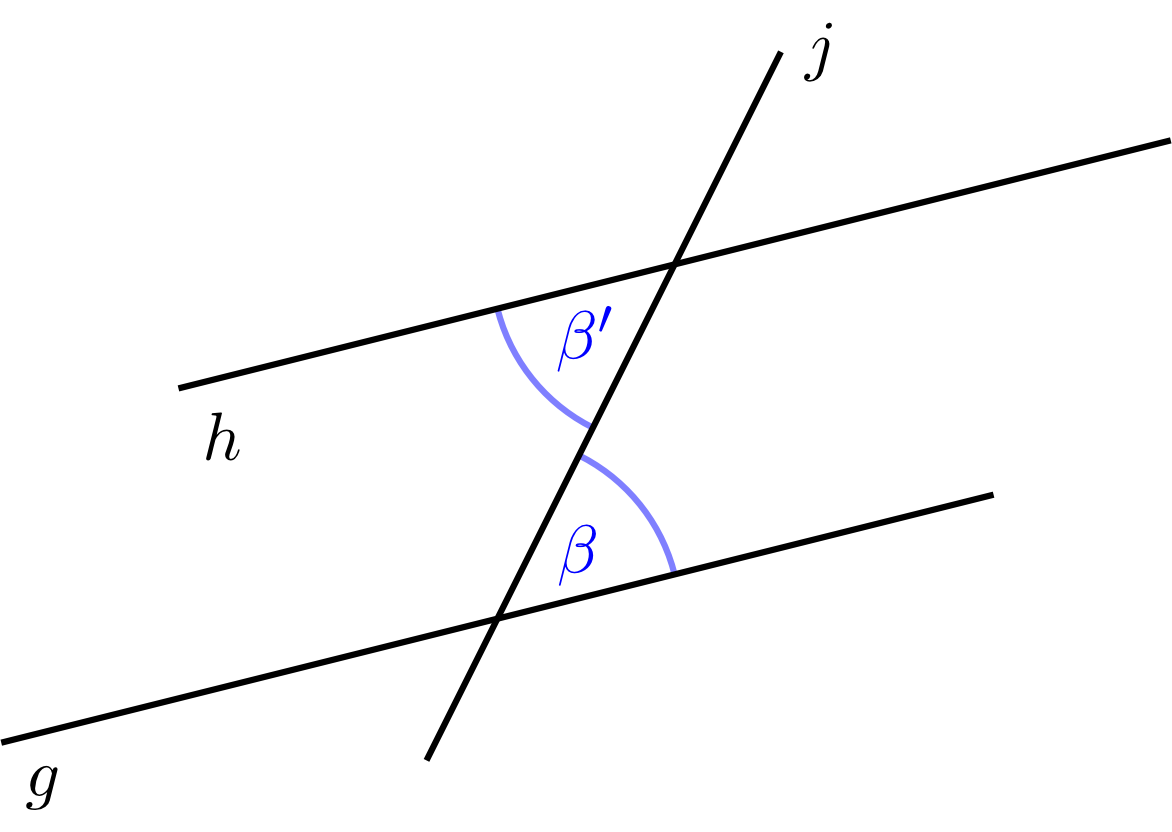
Next, three lines are considered. Two of the three lines are parallel, while the third line is not parallel to the others. It is called a transversal. These lines form eight cutting angles. Four of the eight angles are equal.
 Onlinebrückenkurs Mathematik
Onlinebrückenkurs Mathematik