Chapter 5 Geometry

Section 5.6 Trigonometric Functions: Sine, et cetera

5.6.2 Trigonometry in Triangles

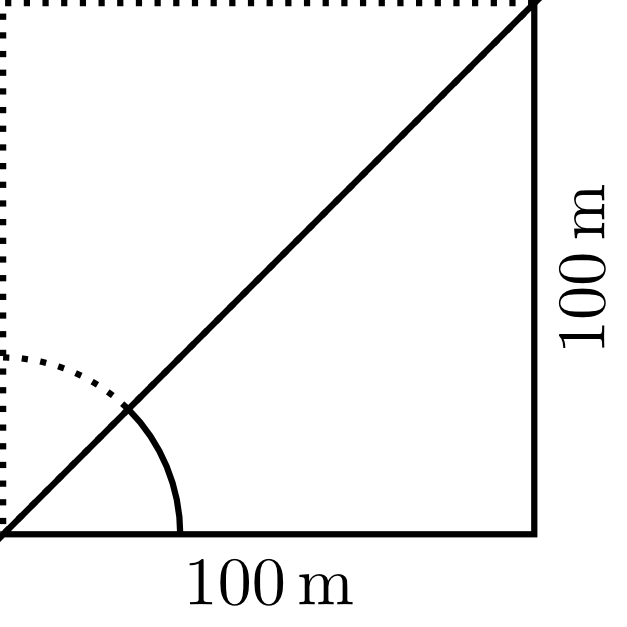
If one drives downhill on a road with a slope of five percent, then the height falls five metres for every 100 metres travelled horizontally. Here, the difference in height is considered in comparison to the horizontal line.

Accordingly, the slope is

100 %

if the difference in height between two positions with a horizontal distance of

100 m

100 m

. Geometrically, the connecting line segment between the two points is a diagonal of a square. Hence, the angle between the horizontal line and the diagonal, i.e. the road on which ones moves, has a degree measure of

45^{\circ}

In other words: An angle of

45^{\circ}

corresponds to a slope of

\frac{100 m}{100 m} = 1

, i.e. the ratio of the horizontal line segment to the vertical line segment is

1

. According to the intercept theorem, this ratio does not depend on the lengths of the individual segments. It only depends on the position of the two rays with respect to each other, i.e. the measure of the angle they enclose. If this assignment of a ratio of the line segments to an angle is also known for other angles, many constructive problems can be solved. For example, for a given angle the height can be determined.
Even the question for the ratio that corresponds to an angle of

30^{\circ}

shows, however, that in general it is not that simple to determine the assignment of a ratio of line segments to an angle. Therefore, the time-consumingly determined values that we considered initially were listed in mathematical tables such that they could be looked up later again easily. Now, these values are available practically everywhere, provided by calculators and computers. The most common assignments of an angle to a ratio of line segments are presented below. They are called circular functions or trigonometric functions. The branch of mathematics dealing with their properties is called trigonometry.

Trigonometric Functions in the Right Triangle 5.6.1

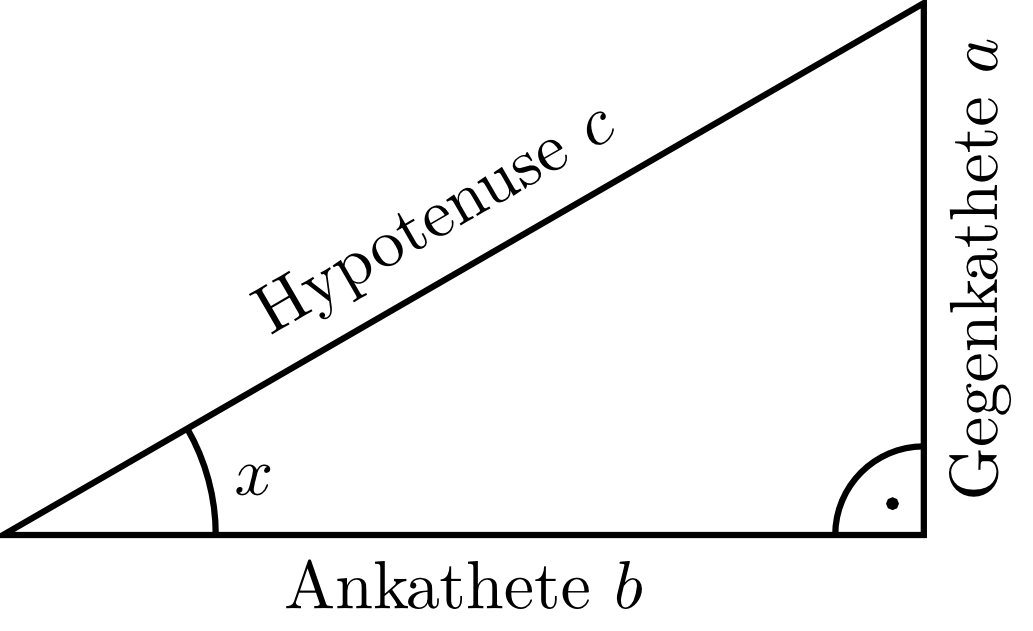
Here, the most common circular functions are described as assignments of ratios of the sides in a right triangle to an angle. The circular functions are also called the trigonometric functions. Here,

x

denotes an angle in a right triangle that is not a right angle. The opposite (side) is the side opposite the angle

x

, and the other leg is called the adjacent (side).

The ratio of the opposite side $a$ to the adjacent side $b$ to an angle is called the tangent function:

$\tan (x) : = \frac{opposite side}{adjacent side} = \frac{a}{b}$
The ratio of the adjacent side $b$ to the hypotenuse $c$ to an angle is called the cosine function:

$\cos (x) : = \frac{adjacent side}{hypotenuse} = \frac{b}{c}$
The ratio of the opposite side $a$ to the hypotenuse $c$ to an angle is called the sine function:

$\sin (x) : = \frac{opposite side}{hypotenuse} = \frac{a}{c}$

The tangent function describes the assignment of the ratio of height to width to the angle of inclination, i.e. the slope. In Chapter 8 this is also relevant in the context to the geometrical interpretation of the derivative.
According to the definition, the tangent function of the angle

α

\tan (α) = \frac{a}{b} = \frac{a}{b} \cdot \frac{c}{c} = \frac{a}{c} \cdot \frac{c}{b} = \frac{\sin (α)}{\cos (α)} .

Thus, it suffices to know the values of sine and cosine to be able to calculate the tangent function.

Example 5.6.2

Let a triangle with a right angle

γ = \frac{π}{2} = 90^{\circ}

be given. The side

c

is of length

5 cm

, and the side

a

is of length

2.5 cm

. Calculate the sine, cosine and tangent function of the angle

α

.
The sine can be calculated immediately from the given values:

\sin (α) = \frac{a}{c} = \frac{2.5 cm}{5 cm} = 0.5 .

To calculate the cosine the length of the side

b

is required - it can be obtained by means of Pythagoras' theorem:

b^{2} = c^{2} - a^{2}

Hence,

\cos (α) = \frac{b}{c} = \frac{\sqrt{c^{2} - a^{2}}}{c} = \frac{\sqrt{{(5 cm)}^{2} - {(2.5 cm)}^{2}}}{5 cm} = 0.866 .

Thus, the tangent of the angle

α

\tan (α) = \frac{\sin (α)}{\cos (α)} = \frac{0.5}{0.866} = 0.5773 .

Exercise 5.6.3

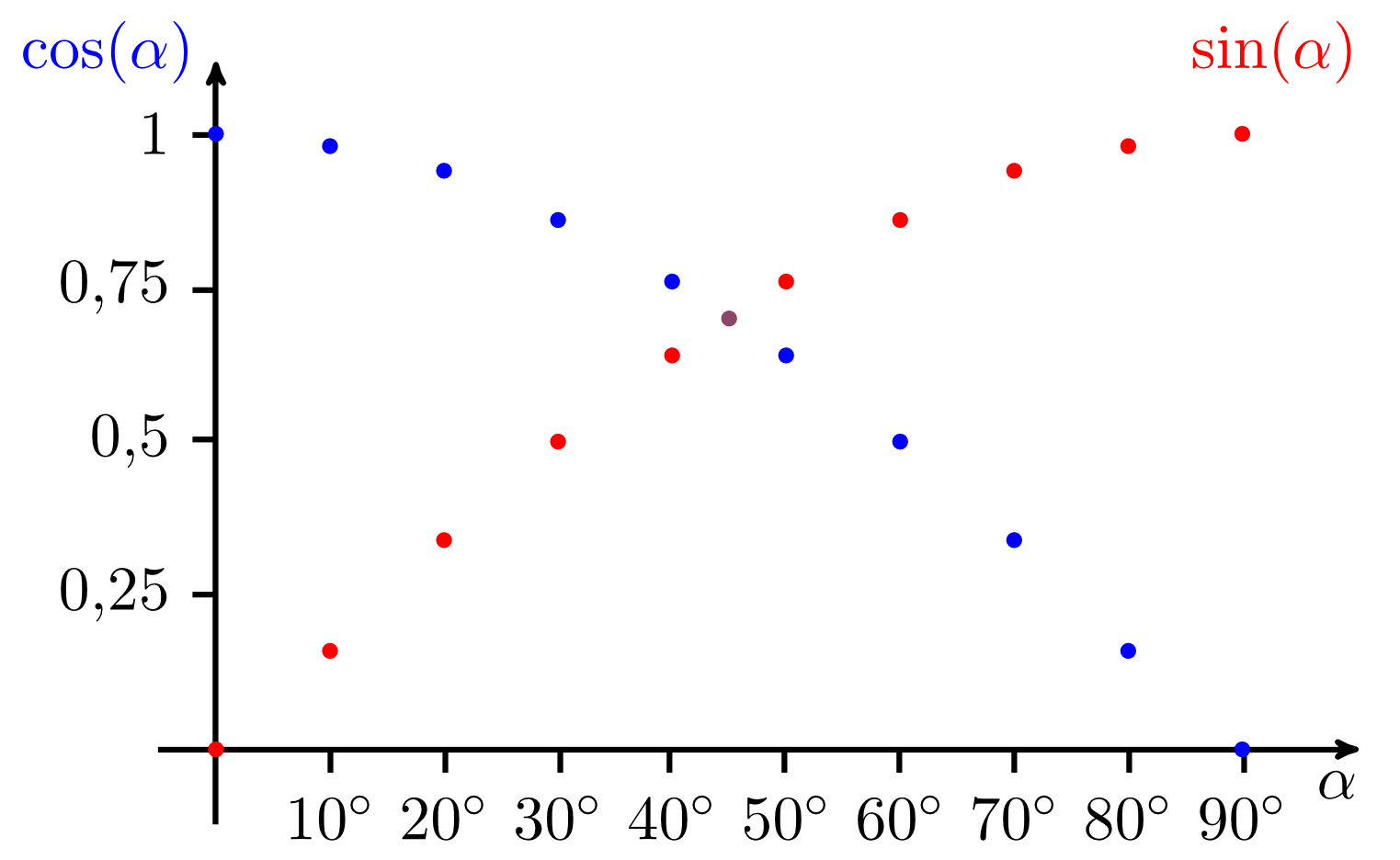
Determine some approximate values of the trigonometric functions sine, cosine and tangent graphically. Let a right triangle with the hypotenuse

c = 5

be given. Use Thales' circle to draw right triangles for the angles

α \in {10^{\circ}; 20^{\circ}; 30^{\circ}; 40^{\circ}; 45^{\circ}; 50^{\circ}; 60^{\circ}; 70^{\circ}; 80^{\circ}} .

Use a drawing scale of

1

unit length

\hat{=} 2 cm

, and fill in the measured values for the sides

a

and

b

in a table. From the measured values, calculate the sine, cosine, and tangent of each angle and decide for which functions also values for

α = 0^{\circ}

and

α = 90^{\circ}

exist. After that, plot the calculated values of sine and cosine against the angle

α

In the process of measurement, errors will always occur! Therefore, the values in your table will be slightly different from the ones given in the table below. The table could look as follows:

$α$	$a$	$b$	$\sin (α)$	$\cos (α)$	$\tan (α)$

0	$0.0$	$5.0$	$0.0$	$1.0$	$0.0$
$10^{\circ}$	$0.8$	$4.9$	$0.160$	$0.98$	$0.1633$
$20^{\circ}$	$1.7$	$4.7$	$0.34$	$0.94$	$0.3617$
$30^{\circ}$	$2.5$	$4.3$	$0.5$	$0.86$	$0.5814$
$40^{\circ}$	$3.2$	$3.8$	$0.64$	$0.76$	$0.8421$
$45^{\circ}$	$3.5$	$3.5$	$0.7$	$0.7$	$1.0$
$50^{\circ}$	$3.8$	$3.27$	$0.76$	$0.64$	$1.1875$
$60^{\circ}$	$4.3$	$2.5$	$0.86$	$0.5$	$1.7200$
$70^{\circ}$	$4.7$	$1.7$	$0.94$	$0.34$	$2.7647$
$80^{\circ}$	$4.9$	$0.8$	$0.98$	$0.160$	$6.1250$
$90^{\circ}$	$5.0$	$0.0$	$1.0$	$0.0$	-

Then, the corresponding diagram looks as follows:

If we once again look closer at the results obtained in the last exercise, we can find different ways to interpret them, and then identify some relations.

With increasing angle $α$ the opposite side $a$ increases and the adjacent side $b$ decreases.
Likewise, $\sin (α) ~ a$ and $\cos (α) ~ b$ .
With increasing angle $α$ the opposite side $a$ increases to the same extent as the adjacent side $b$ decreases with the angle $α$ decreasing from $90^{\circ}$ . In the Thales circle, the two triangles with the opposite values of $a$ and $b$ are two solutions for the construction of a right triangle with a given hypotenuse and a given altitude (see also Example 5.3.7).
In the right triangle the adjacent side of the angle $β = 90^{\circ} - α$ is the same side as the opposite side of the angle $α$ (and vice versa). Thus,

$\sin (α) = \cos (90^{\circ} - α) = \cos (\frac{π}{2} - α)$
and

$\cos (α) = \sin (90^{\circ} - α) = \sin (\frac{π}{2} - α) .$
For $α = 45^{\circ}$ the opposite side and adjacent side are equal, and thus sine and cosine are equal as well. This observation was used at the beginning of this section for the determination of the slope.
The tangent function, i.e. the ratio of $a$ to $b$ , increases with increasing angle $α$ from zero to "infinity".

In the following example we will continue our considerations from the beginning of this section and use a triangle with an angle of

45^{\circ}

to calculate the value of the corresponding sine value exactly.

Example 5.6.4

Calculate the sine of the angle

α = 45^{\circ}

now exactly, i.e. unlike as in Exercise 5.6.3, where the sine was calculated from measured (and hence error-prone) values.
If in a right triangle with

γ = 90^{\circ}

the angle

α

is equal to

45^{\circ}

, then, because of the formula for the sum of interior angles in a right triangle,

α + β + γ = π = 180^{\circ}

, the angle

β

also needs to be equal to

45^{\circ} = π / 4

, and the two legs

a

and

b

are of equal length. A triangle with two sides of equal length is called an isosceles.

We have:

\sin (α) = \sin (45^{\circ}) = \frac{a}{c} .

Moreover:

a^{2} + b^{2} = 2 a^{2} = c^{2} \Rightarrow c = \sqrt{2} \cdot a

\Rightarrow \sin (45^{\circ}) = \sin (π / 4) = \frac{a}{\sqrt{2} \cdot a} = \frac{1}{2} \cdot \sqrt{2} .

In Exercise 5.6.3 the value of the sine of

45^{\circ}

was approximated by a value of

0.7

which is quite close to the actual value of

\frac{1}{2} \cdot \sqrt{2}

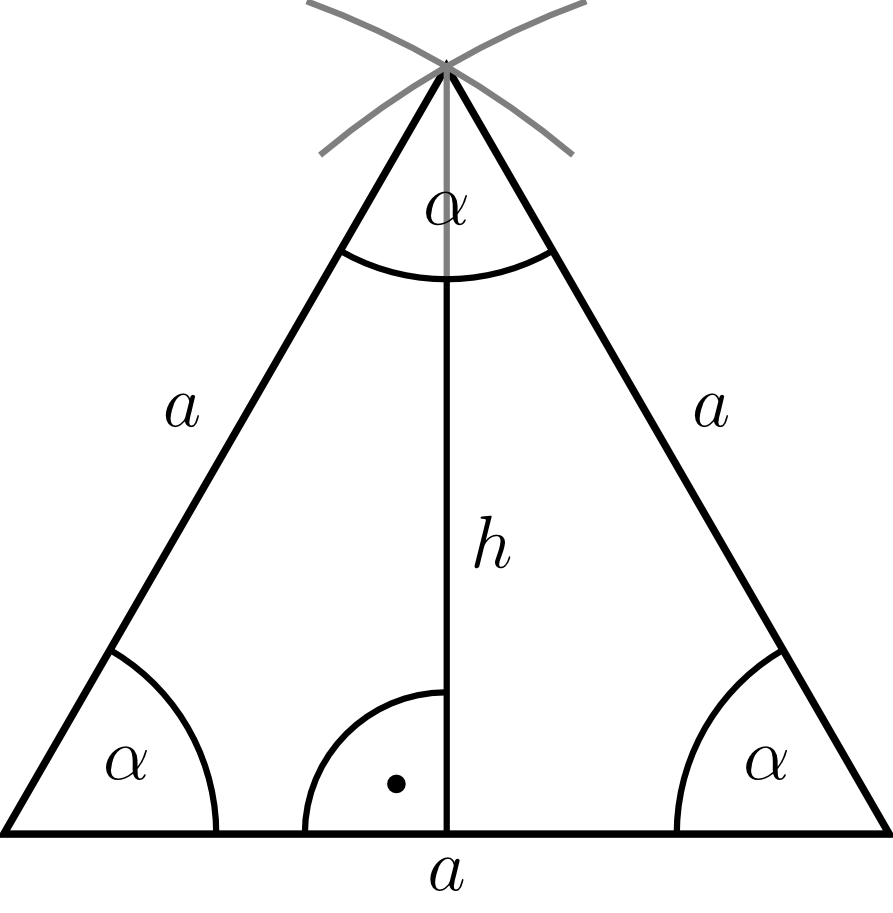
In the next example we will calculate the sine of the angle

α = 60^{\circ}

. For this purpose, we first do not consider a right triangle but an equilateral triangle. By a clever decomposition of the triangle and by using another "auxiliary quantity" we will obtain the required result.

Example 5.6.5

Consider a equilateral triangle to calculate

\sin (60^{\circ})

. As the name implies, the sides of this triangle are all of equal length, and the angles are also all of the same magnitude, namely

α = β = γ = \frac{180^{\circ}}{3} = 60^{\circ} = \frac{π}{3}

. According to the theorem for congruent triangles "sss", the triangle is defined uniquely by the specification of a side

a

. This triangle is constructed by drawing the side

a

and then drawing a circle with radius

r

around both endpoints of the side. Now, the intersection point of the two circles is the third vertex.

This triangle is not right-angled. If an altitude

h

is drawn on one of the sides

a

, the triangle can be divided into two congruent right triangles.
We have:

\sin (α) = \sin (60^{\circ}) = \frac{h}{a} .

According to Pythagoras' theorem we have

{(\frac{a}{2})}^{2} + h^{2} = a^{2} .

Therefore,

h^{2} = \frac{3}{4} a^{2} and hence h = \frac{1}{2} \sqrt{3} \cdot a .

As a result we obtain the required value

\sin (60^{\circ}) = \sin (\frac{π}{3}) = \frac{h}{a} = \frac{1}{2} \cdot \sqrt{3} .

From this triangle the sine of another angle can also be calculated: the altitude

h

bisects the above angle such that in the two congruent smaller triangles the above angle is

30^{\circ} = \frac{π}{6}

. Now we have

\sin (30^{\circ}) = \sin (\frac{π}{6}) = \frac{a / 2}{a} = \frac{1}{2} .

Exercise 5.6.6

Calculate the exact value of the cosine of the angles

α_{1} = 30^{\circ}

α_{2} = 45^{\circ}

, and

α_{3} = 60^{\circ}

. To do this, use the results obtained in the example above and in Exercise 5.6.3.

From Exercise 5.6.3 it is known that

\cos (α) = \sin (90^{\circ} - α)

. With the results obtained in the example above it follows

\begin{matrix} \cos (30^{\circ}) & = & \sin (90^{\circ} - 30^{\circ}) = \sin (60^{\circ}) = \frac{1}{2} \cdot \sqrt{3}, \\ \cos (45^{\circ}) & = & \sin (90^{\circ} - 45^{\circ}) = \sin (45^{\circ}) = \frac{1}{2} \cdot \sqrt{2}, \\ \cos (60^{\circ}) & = & \sin (90^{\circ} - 60^{\circ}) = \sin (30^{\circ}) = \frac{1}{2} . \end{matrix}

The following small table lists the values for frequently used angles: In the first row denoted by

x

the angle is given in degree measure, and in the last row denoted by

α

the angle is given in radian measure.
\[ \begin{array}[t]{l|*{5}{c}} x & 0 & \tfrac{\pi}{6} & \tfrac{\pi}{4} & \tfrac{\pi}{3} & \tfrac{\pi}{2} \\[1mm] \hline \sin & 0 = \frac{1}{2} \cdot \sqrt{0} & \frac{1}{2} = \frac{1}{2} \cdot \sqrt{1} & \frac{1}{2} \cdot \sqrt{2} & \frac{1}{2} \cdot \sqrt{3} & \frac{1}{2} \cdot \sqrt{4} = 1 \\[1mm] \cos & 1 = \frac{1}{2} \cdot \sqrt{4} & \frac{1}{2} \cdot \sqrt{3} & \frac{1}{2} \cdot \sqrt{2} & \frac{1}{2} \cdot \sqrt{1} = \frac{1}{2} & \frac{1}{2} \cdot \sqrt{0} = 0 \\[1mm] \tan & 0 & \frac{\sqrt{3}}{3} & 1 & \sqrt{3} & - \\[1mm] \hline \alpha & 0^{\circ} & 30^{\circ} & 45^{\circ} & 60^{\circ} & 90^{\circ} % \end{array} \]
You should learn these values by heart. The values of the trigonometric functions for other angles are listed in tables or saved in your calculator.
Hence, a height can be calculated very easily from an angle and a distance. Namely, if

s

is the distance of a building with a flat roof, which is observed at an angle of

x

, then from

\tan (x) = \frac{h}{s}

we have

h = s \cdot \tan (x)

. Likewise, sine and cosine can be used to calculate lengths. This relation between angles and lengths is often used.
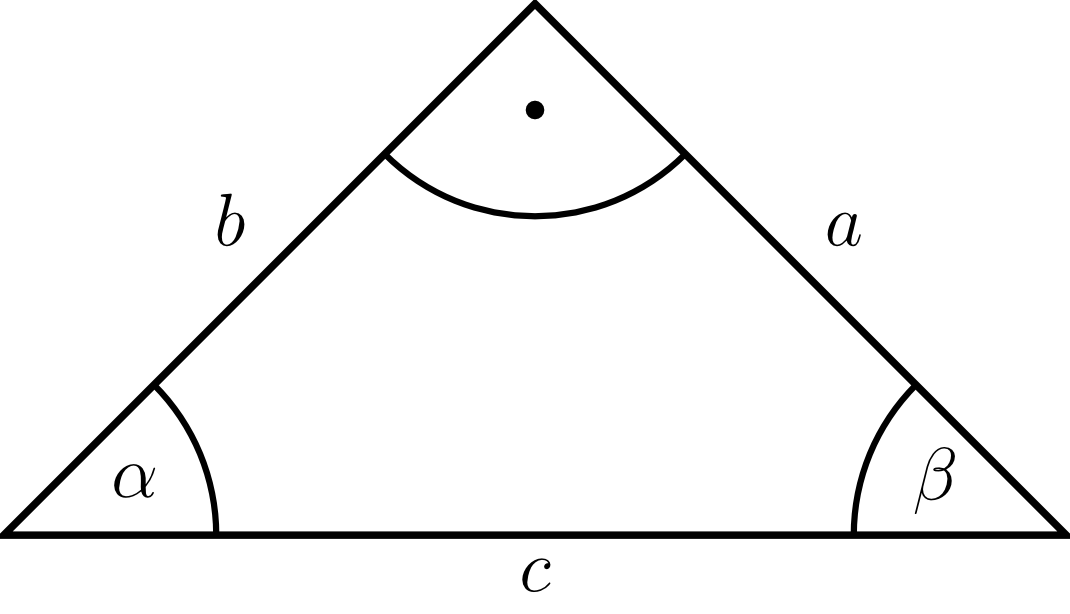
For example, an area can be calculated in this way even if the required length is not given directly. In the following example, the altitude of a triangle is to be calculated. Since the

h

starting in a vertex

C

is perpendicular to the line of the opposite side

c = \overline{A B}

, the vertices of

h

and

A

B

, respectively, form a right triangle. If an angle and the adjacent side are given, then the altitude can be calculated from

\sin (α) = \frac{h}{b}

or from

\sin (β) = \frac{h}{a}

, using standard notation.

Exercise 5.6.7

Calculate the area

F

of a triangle with the sides

c = 7

b = 3

, and the angle

α = 30^{\circ}

between the two sides

c

and

b

.
Result:

F

=

The area

F

can be calculated from

F = \frac{1}{2} \cdot c \cdot h_{c}

, where we still need to determine

h_{c}

. From

\sin (α) = \frac{h_{c}}{b}

we have

h_{c} = b \cdot \sin (α) = 3 \cdot \sin (30^{\circ}) = 3 \cdot \frac{1}{2} .

Hence,

F = \frac{1}{2} \cdot c \cdot b \cdot \sin (α) = \frac{1}{2} \cdot 7 \cdot 3 \cdot \frac{1}{2} = \frac{21}{4} .

Onlinebrückenkurs Mathematik

1. Elementary Arithmetic

2. Equations in one Variable

3. Inequalities in one Variable

4. System of Linear Equations

5. Geometry

6. Elementary Functions

7. Differential Calculus

8. Integral Calculus

9. Objects in the Two-Dimensional Coordinate System

10. Basic Concepts of Descriptive Vector Geometry

11. Language of Descriptive Statistics