Chapter 5 Geometry

Section 5.3 All about Triangles

5.3.2 Triangles


Many statements on geometric figures and solids arise from the properties of triangles. A triangle is the "simplest closed figure" which can be determined by three non-collinear points (i.e. the points do not lie on a single straight line).
First, we will present the important terms. Then we will determine under which conditions a triangle is uniquely defined and how individual angles and sides can be calculated. Here the intercept theorems are an important tool, since they can also be considered as statements on relations between different triangles.
In Section 5.6 we will then investigate functional relations between side lengths and angles enabling us to answer advanced questions relevant to applications.
Triangle 5.3.1

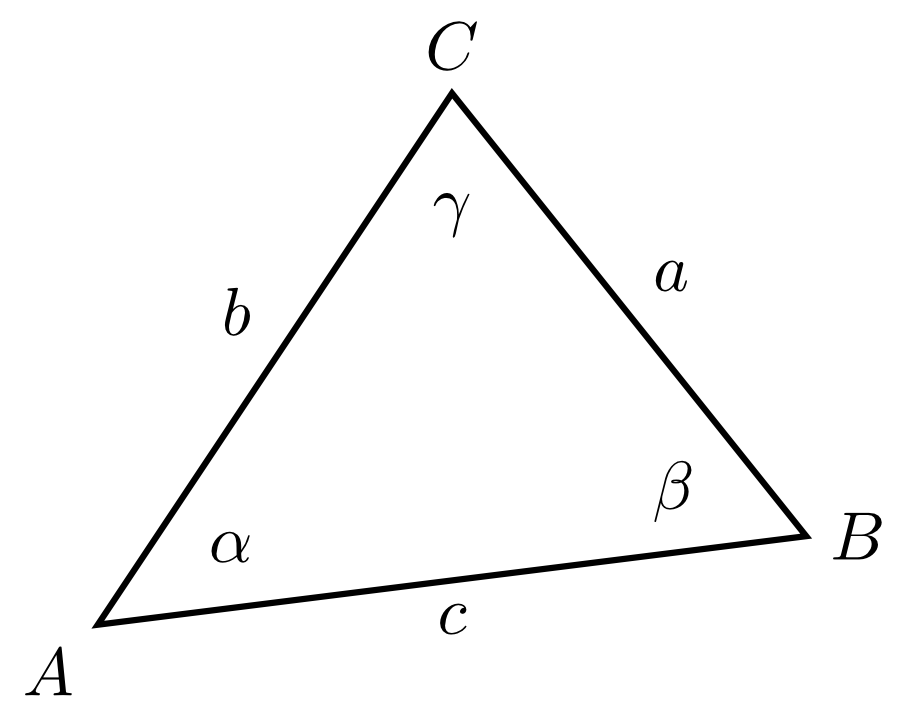
A triangle is constructed by joining three non-collinear points A, B, and C. The triangle is denoted by ABC.
  • The three points are called the vertices of the triangle, and the three lines are called the sides of the triangle.
  • Any two sides of the triangle form two angles. The smaller angle is called the interior angle (or simply angle for short) and the greater angle is called the exterior angle.
  • The sum of the three interior angles is always 180 ∘ or π.


The vertices and sides of a triangle are often denoted as follows: vertices are denoted by upper-case Latin letters in mathematical positive direction (counter-clockwise). The side opposite a vertex is denoted by its lower-case Latin letter, and the interior angle of the vertex is denoted by the corresponding lower-case Greek letter.
Since exterior angles are far less important than interior angles, the interior angles are simply called the angles of the triangle.
The sum of all (interior) angles is always 180 ∘ or π. Hence, at most one angle can be equal to or greater than 90 ∘ or π 2 . Consequently, triangles are classified according to their greatest interior angle into three types:
Names of Triangles 5.3.2
Triangles are named according to their angles as follows:
  • A triangle that only has angles less than  π 2 is called an acute.
  • A triangle that has a right angle is called a right-angled triangle or simply a right triangle.
    In a right triangle the two sides enclosing the right angle are called the catheti or legs, and the side opposite to the right angle is called the hypotenuse.
  • A triangle that has an angle greater than  π 2 is called an obtuse.

As an example, let us consider the simple structure of a car jack with the shape of a triangle (see figure below): It consists of two rods connected by a joint. The two other endpoints of the rods can be pulled together. The greater the angle of a rod with respect to the street is, the higher the joint is above the ground.

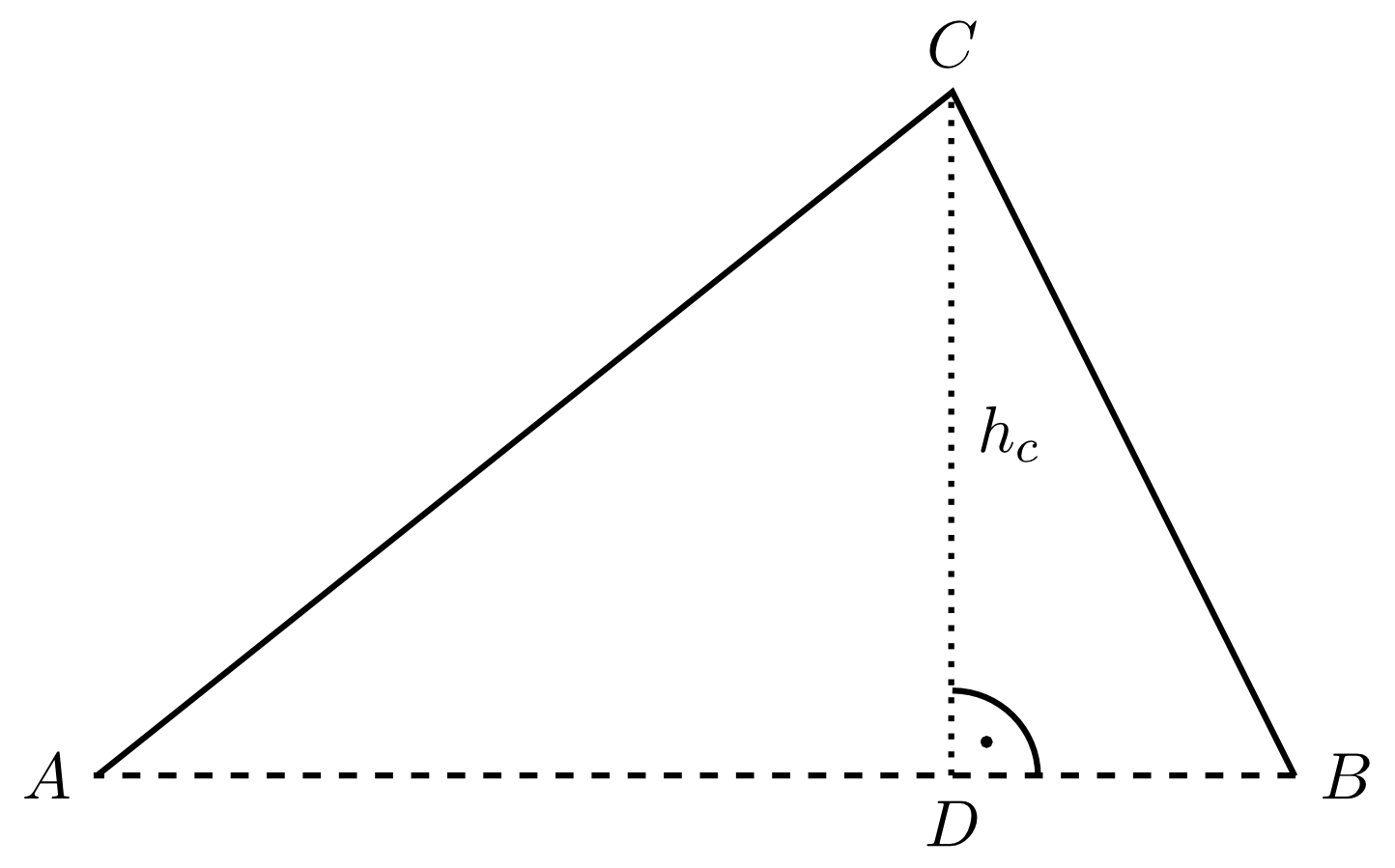
Thus, in a triangle ABC the shortest line segment between vertex C and the line defined by the side c opposite to C is called the altitude (or height) of the triangle hc on the (base) side c. The second endpoint D of the line segment hc is called the perpendicular foot. The altitudes ha and hb are defined accordingly.
One can also say that altitudes are those line segments that are perpendicular to the line of a side and have the vertex opposite to the relevant side as an endpoint.
: