Chapter 5 Geometry

Section 5.4 Polygons, Area and Circumference

5.4.3 Polygons


For triangles, even one vertex or side contributes to the essential properties of the whole triangle, for example, one vertex with a right angle. For quadrilaterals, a single vertex no longer has such strong specifying properties. Instead, there is a greater variety of shapes. If "many" points are connected to a closed figure by line segments, there are many possibilities to create various figures and even to approximate round shapes.

In this general case, a detailed classification as for triangles or quadrilaterals is barely possible. The new possibilities such as the approximation of round shapes do also lead to new interesting questions. One does not consider single polygons but construction principles for a series of many polygons. On the other hand, every polygon can be divided into triangles if required, as we have seen already for quadrilaterals. Thus, a property of a single vertex is often considered in terms of what this means for the polygon in the whole.
For classification, the question is convenient whether a certain condition is satisfied by all vertices or not, and what this means for the polygons. For example, polygons are classified according to the magnitudes of their angles, e.g. whether all angles of the vertices are less than π or 180 ∘ . If so, all diagonals pass through the inside of the polygon. Otherwise, at least one diagonal exists in the outside.
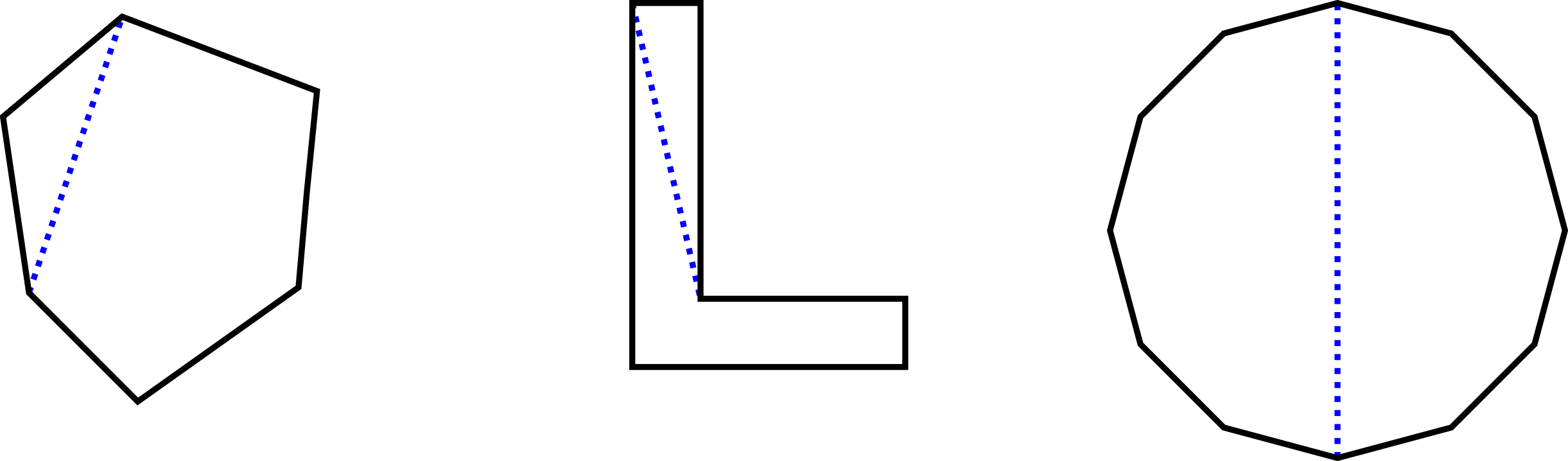
The figure above shows examples of polygons exhibiting different properties. In the polygon to the left all (interior) angles are less than π or 180 ∘ . In this case the polygon is said to be convex. In contrast, the polygon in the middle contains a vertex with an angle greater than π or 180 ∘ . In the polygon to the right all angles are equal, leading to a very evenly shaped polygon.
Polygons 5.4.8

Let n points in the plane be given, where n is a natural number with n≥3. Here, we consider polygons constructed by connecting points by line segments such that a closed, non-self-intersecting (simple) path is formed, and every point is adjacent to exactly two segments, where every three points connected by successive segments are to be non-collinear.
A polygon is also called an n-gon.
  • The n points that are connected are called the vertices of the polygon, and the n connecting line segments are called the sides of the polygon.
  • Every polygon can be divided into (n-2) non-overlapping triangles. Hence, the sum of the interior angles of a polygon is (n-2)·π or (n-2)·180 ∘ .
  • Line segments connecting two vertices not adjacent to the same side of the polygon are called the diagonals of the polygon.

Further statements hold for polygons with sides of equal length and equal interior angles. For n=3, these are equilateral triangles, end for quadrilaterals these are squares.
Regular Polygons 5.4.9
A polygon that is equilateral (all sides have the same length) and equiangular (all angles are equal in measure) is called a regular polygon or a regular n-gon.

Honeycombs are - when seen from above - approximately regular hexagons.

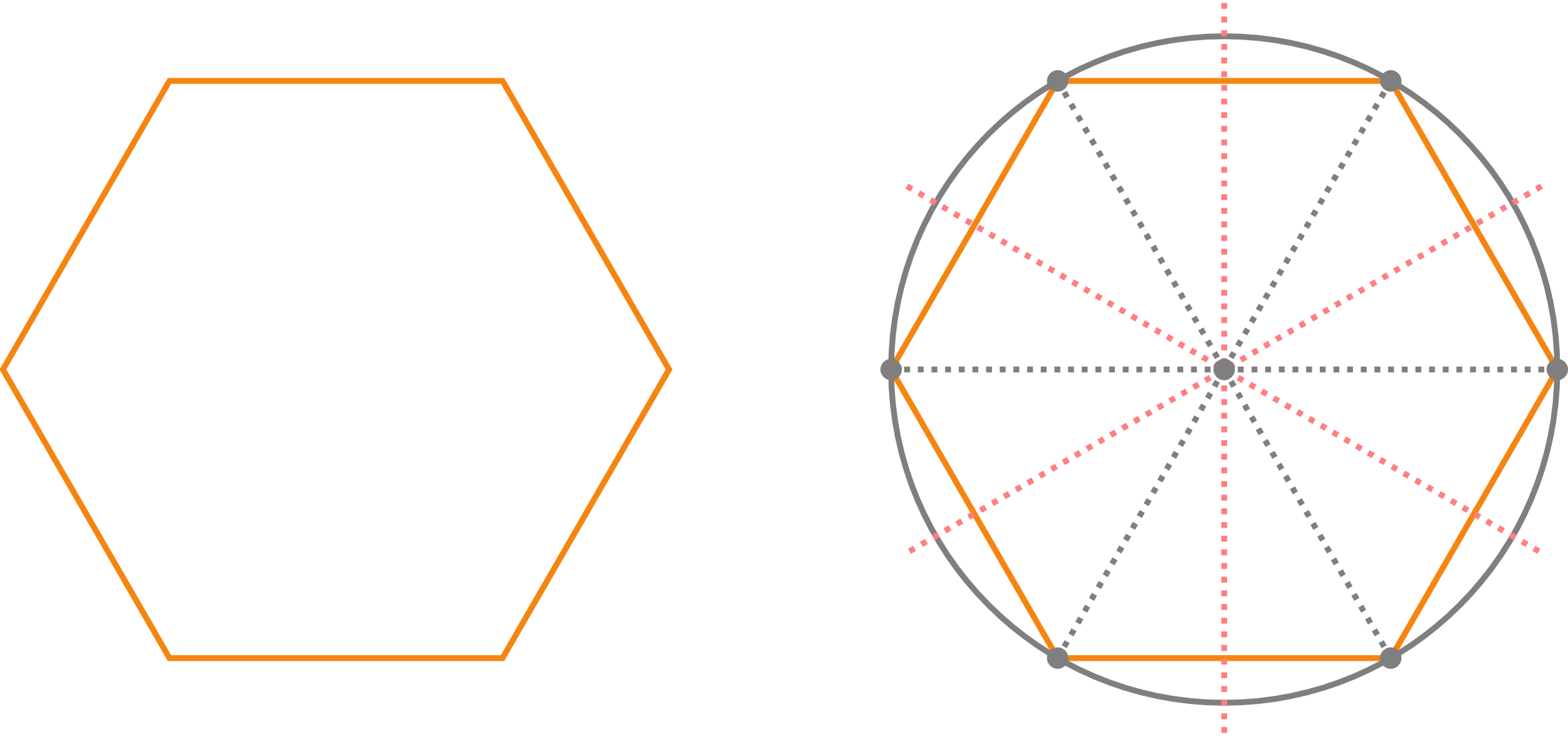
Regular polygons have various symmetry properties. All lines perpendicular to the sides, passing through the midpoint of the respective side, intersect in a point M. Reflecting a polygon across such a line maps it onto itself.
Furthermore, regular polygons have rotational symmetry, i.e. a n-gon maps onto itself if it is rotated around M by an angle of 2π n .
The vertices of a regular polygon have all the same distance from M and thus lie all on a circle around  M.
: