Chapter 5 Geometry
Section 5.2 Angles and Angle Measurement5.2.3 Angle Measurement
We already explained the notation for the angle defined by rotating counter-clockwise to . This explanation provides an idea of how to measure angles, i.e. how to compare angles quantitatively.
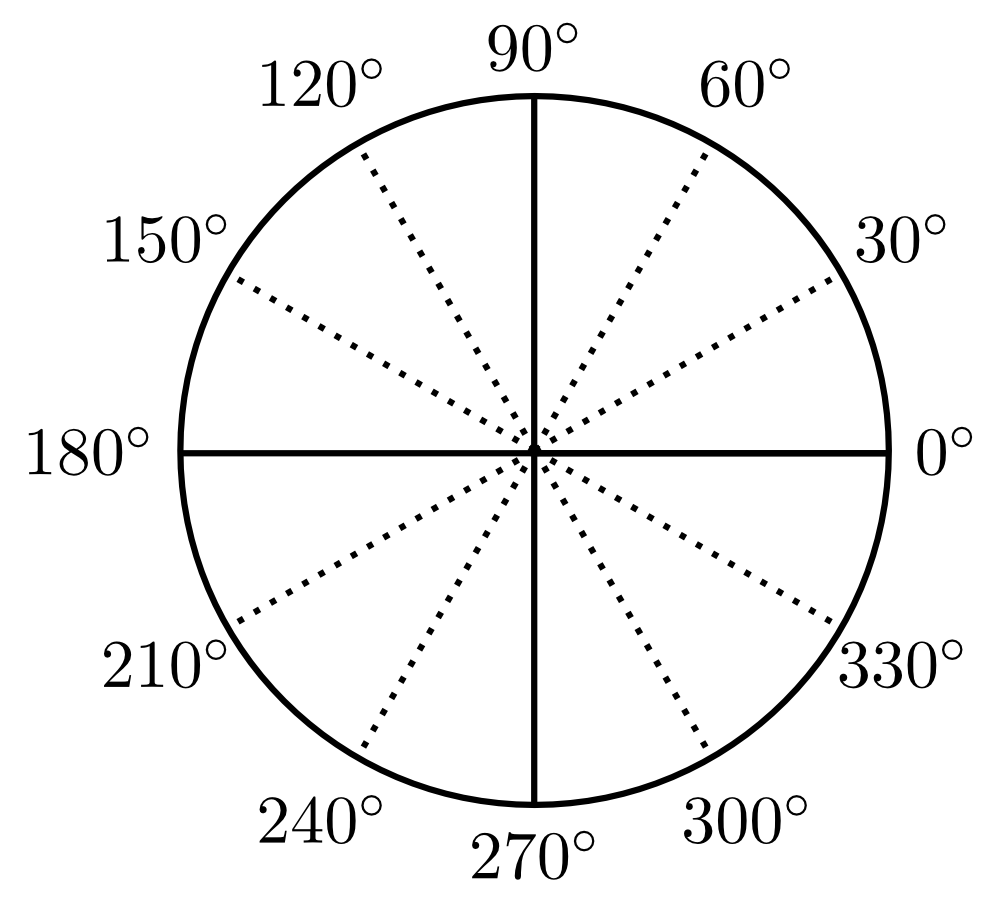
Think of the face of an analogue watch with its twelve evenly spaced hour marks. Likewise, the circumference of a circle can be evenly subdivided. In this way, a certain scale for angles is obtained. Depending on the applied scaling, the magnitude of an angle can be specified in different units.
Degree Measure.
A disk is subdivided into equal segments. A rotation by one segment defines an angle of degree. This is written as . The figure below shows angles of multiples of .
Radian Measure.
In ancient Babylonia, Egypt, and Greece people had already observed that the ratio of the circumference of a circle to its diameter is always the same, and hence circumference and diameter of a circle are proportional to each other. This ratio is called .
The Number 5.2.6
Let a circle with circumference and diameter be given. Then, the ratio of the circumference of a circle to its diameter is
where is the radius of the circle.
The number is not a rational number. It cannot be expressed as a finite or periodic decimal fraction. From numerical calculations we know that the value of is approximately .
where is the radius of the circle.
The number is not a rational number. It cannot be expressed as a finite or periodic decimal fraction. From numerical calculations we know that the value of is approximately .
If the circle has a radius of exactly , the circumference is . Now, for the radian measure the circumference of a circle with radius is subdivided. For the radian measure of an angle the length of an arc "cut" by this angle is used. As a result, the radian measure assigns to every angle a number between and . In scientific applications, the symbol rad is used to express explicitly that the angle is measured in radian measure.
Radian Measure 5.2.7
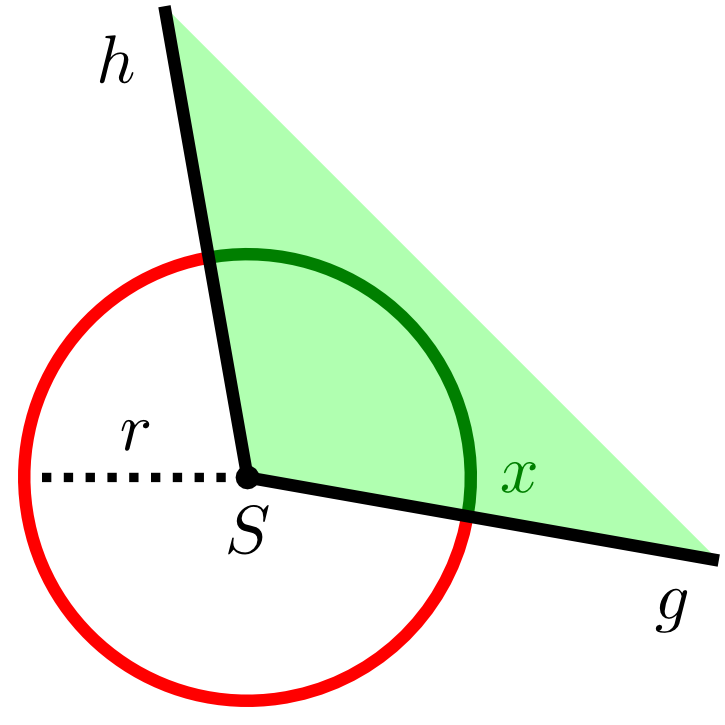
Let and be two half-lines starting in the same initial point and enclosing the angle . If a circle with radius is drawn around , the two half-lines cut the circle into two pieces. Now, the angle is described by the one arc that transforms into by a counter-clockwise rotation (indicated by a green line in the figure below). In other words, vertex is always on the left if one moves on the arc from towards .
The length of the arc is the radian measure of the angle .
The length of the arc is the radian measure of the angle .
By means of an angle measure (such as the radian and degree measures introduced previously), angles can simply be classified into different types and named accordingly.
For repetition and completeness, all names, including ones previously discussed, are listed below.
Names of Different Types of Angles 5.2.8
For angles whose radian measure is in a certain range, the following names are introduced:
Two half-lines are said to be perpendicular to each other if they form a right angle.
Two half-lines form a line if they enclose an angle of radian measure .
- An angle with a radian measure greater than and less than is called an acute angle.
- An angle with a radian measure of exactly is called a right angle.
- An angle with a radian measure greater than and less than is called an obtuse angle.
- An angle with a radian measure greater than and less than is called a reflex angle.
Two half-lines are said to be perpendicular to each other if they form a right angle.
Two half-lines form a line if they enclose an angle of radian measure .
From the radian measure of the angle , the radian measure of the angle can also be determined. From definition 5.2.7 it is known that
In the figure of definition 5.2.7 the radian measure of the angle is the length of the red arc of the circle with radius .
The wording in the last sentences might seem awkward. The reason for that lies probably in the fact that we do distinguish precisely between an angle and its measure, e.g. the radian measure in this case.
When it comes to calculating a required value for line segments, the same notation is often used for a segment and its length. Mostly this is clear, and it helps to describe or to illustrate a problem efficiently. Importantly, the unit of the angle has to be known or explicitly specified. Often, such an agreement - a so-called convention - is also used if it is known from the context that a certain angle has to be calculated using a certain angle measure.
The value of an angle can be converted from radian measure to degree measure (and vice versa) by considering the ratios of its value to the value of the complete angle in the respective angle measure.
The conversion from radian measure to degree measure is described below.
Relation between Radian Measure and Degree Measure 5.2.10
Let and be two half-lines enclosing the angle . The radian measure of the angle is denoted by and the degree measure of the angle is denoted by .
Then, the ratio of to equals the ratio of to , and thus:
Hence,
Then, the ratio of to equals the ratio of to , and thus:
Hence,
Therefore, the values in radian measure are proportional to the ones in degree measure. Thus, the conversion using the respective proportionality factors and is very simple.
Exercise 5.2.11
The angle equals in degree measure. Calculate the angle in radian measure:
.
Enter as pi. Alternatively, you can enter your result rounded to three decimal digits.
.
Enter as pi. Alternatively, you can enter your result rounded to three decimal digits.
Exercise 5.2.12
The angle equals in radian measure. Find its value in degree measure.
.
.
Exercise 5.2.13
The values of the six angles are specified either in degree measure or in radian measure. Convert their values to the other measure.
Enter as pi. Alternatively, you can enter your result rounded to three decimal digits.
| Radian measure | | | | |||
| Degree measure | | | |
Enter as pi. Alternatively, you can enter your result rounded to three decimal digits.
 Onlinebrückenkurs Mathematik
Onlinebrückenkurs Mathematik