Chapter 5 Geometry

Section 5.5 Simple Geometric Solids

5.5.2 Simple Geometric Solids

Points are the simplest basic geometric objects. Translations of points result in line segments, and transformations such as translation or rotation of line segments result in simple geometric figures. For example, polygons and circles are obtained in a way described above.
If figures are shifted or rotated out of their plane, then new objects are created that are denoted as solids. In this section some simple solids will be described, whose shapes can be identified easily in many everyday objects and technical constructions.

Example 5.5.1

Let us consider a rectangle and shift it perpendicular to the drawing plane. In this way, a rectangular cuboid (or informally a rectangular box) is constructed. Its surface consists of the given rectangle and a copy of that (two faces). Four further rectangles (faces) are formed by the four sides of the given rectangle.

Taking any polygon and shifting it perpendicular to the drawing plane, results in a solid that is called a prism. The term also denotes a transparent optical element of this shape used to refract light waves. Because the angle of refraction depends on the wavelength (i.e. the colour of the light), the different wave lengths of seemingly white light are refracted differently. In this way, the different colours of white light become visible.

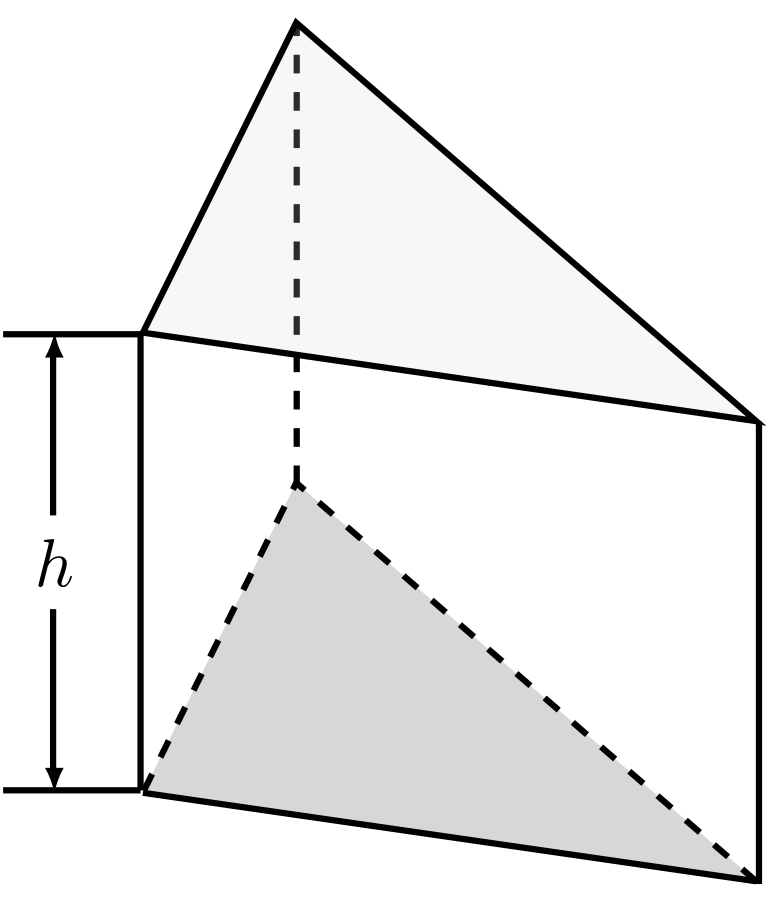
Prism 5.5.2

Let a polygon

G

be given. A prism is a solid resulting from a perpendicular translation of a polygon

G

by a line segment of length

h

. The two faces, i.e. the given polygon and the shifted copy of this polygon, are then called the base faces. They are parallel to each other. All other faces together form the lateral surface

M

The figure above shows a prism with a triangle as its base. The other faces adjacent to the base face are rectangles.
The volume

V

of the prism is the product of the area of the polygon

G

and the height

h

: We have

V = G \cdot h

.
The area

O

of the surface is the sum of twice the area of the base face

G

and the area of the lateral surface

M

. If

U

is the circumference of the given polygon, we have

O = 2 \cdot G + M = 2 \cdot G + U \cdot h

In the introductory example a rectangular cuboid was described. Using the definition above, it can be considered as a special case of a prism, namely a prism with a rectangle as its base face. If all faces are squares, the prism is called a cube.
The construction principle can be varied in different ways. For example, the polygon can be replaced by a disk that is shifted. By a perpendicular translation of the disk a solid is created that is especially symmetric, namely a cylinder. A tunnel drilling machine creates - if considered in a simplified manner - a cylindrical tube.

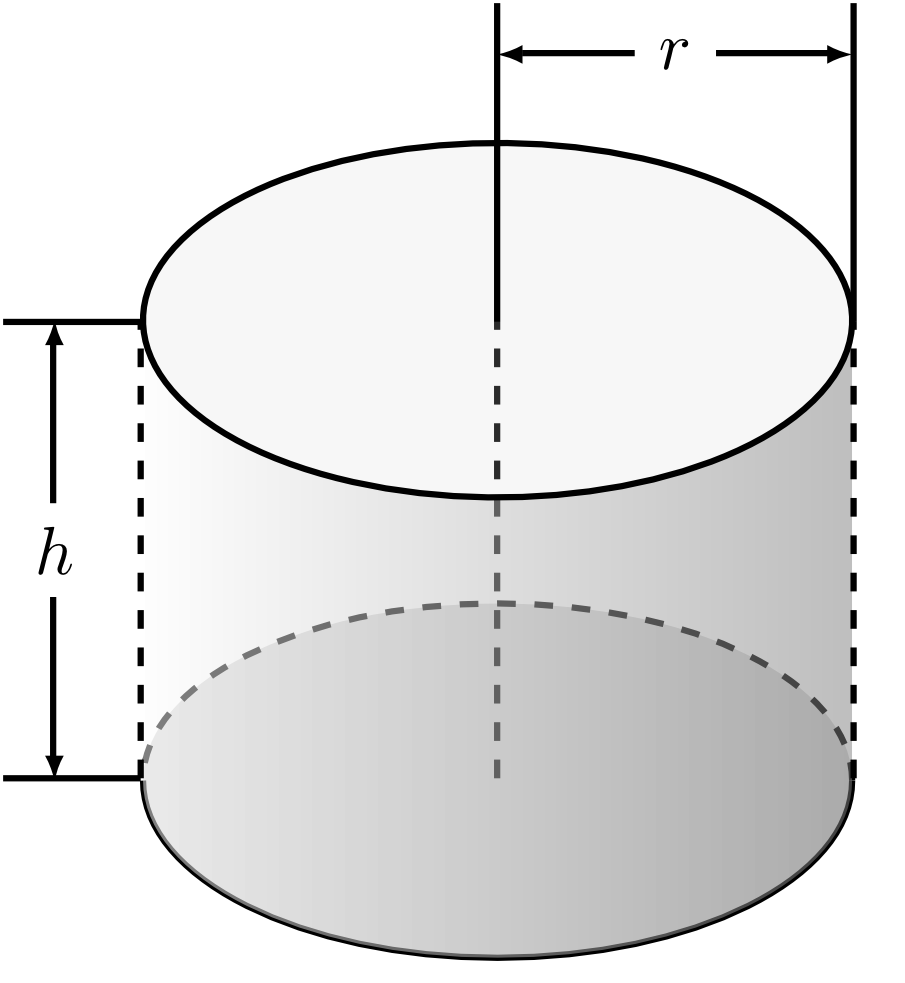
Cylinder 5.5.3

Let a disk

G

be given. A cylinder is a solid created by a perpendicular translation of a disk

G

by a line segment

h

. The two faces, i.e. the given disk and its copy, are then called the base faces of the cylinder. They are parallel to each other. The curved part of the surface between the two disks forms the lateral face

M

of the cylinder.

The volume

V

of the cylinder is the product of the area of the disk

G

with radius

r

and the height

h

of the cylinder:

V = G \cdot h = π \cdot r^{2} \cdot h

.
The area

O

of the surface is the sum of twice the area of the disk

G

and the area of the lateral surface

M

. With the circumference

U = 2 \cdot π \cdot r

of the disk we have

O = 2 \cdot G + M = 2 \cdot π \cdot r^{2} + 2 \cdot π \cdot r \cdot h = 2 \cdot π \cdot r \cdot (r + h)

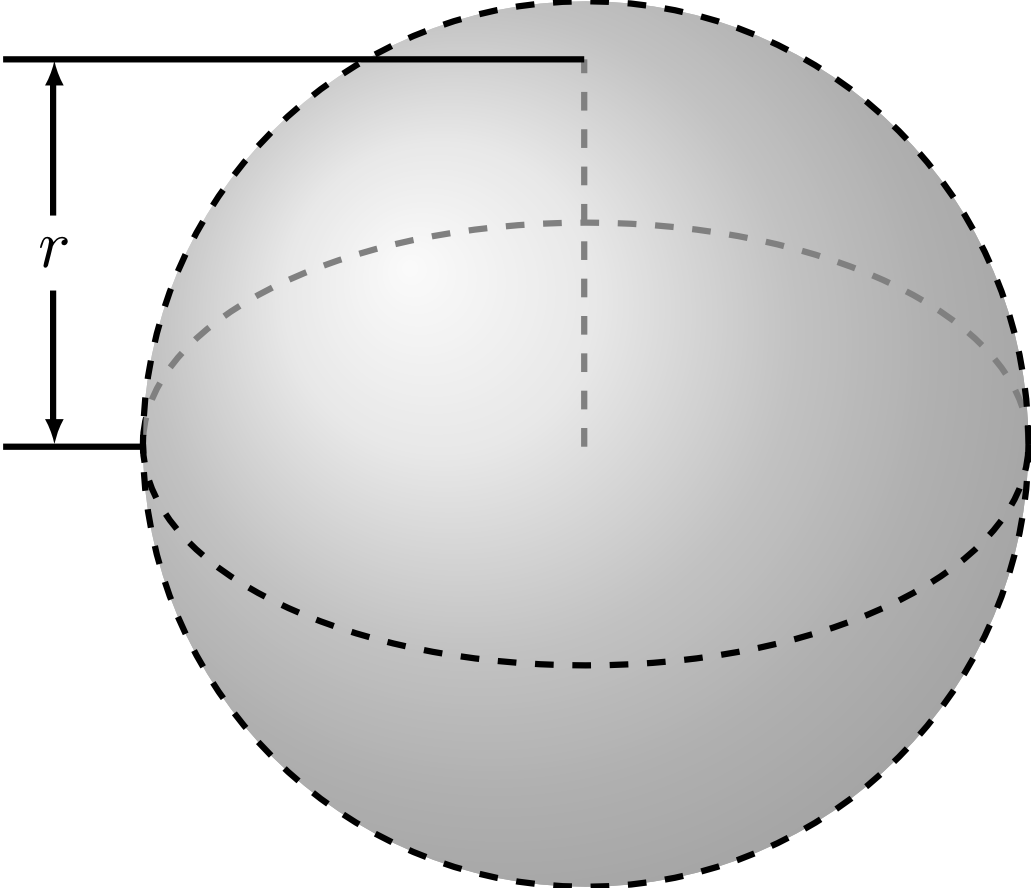
If the disk is not translated but rotated, where the axis of rotation passes trough the centre of the disk and one of its boundary points, then the resulting solid is a sphere.

Sphere 5.5.4

Let a disk with centre

M

and radius

r

be given. If the disk

M

is rotated around an axis trough

M

and a boundary point of the disk, the resulting solid is a sphere with radius

r

The volume

V

of the sphere is

V = \frac{4}{3} \cdot π \cdot r^{3}

.
The area

O

of the surface is given by

O = 4 \cdot π \cdot r^{2}

A sphere can also be described as a solid consisting of all points that have a distance less than or equal to

r

from

M

(see also Chapter 10).
In this approach, a prism is a solid consisting of all points that lie on a connecting line between the base face and its copy.
In the following, two variations of this approach will be considered. We start again with a polygon as base face. Moreover, instead of a copy of the base face, only a point is given.

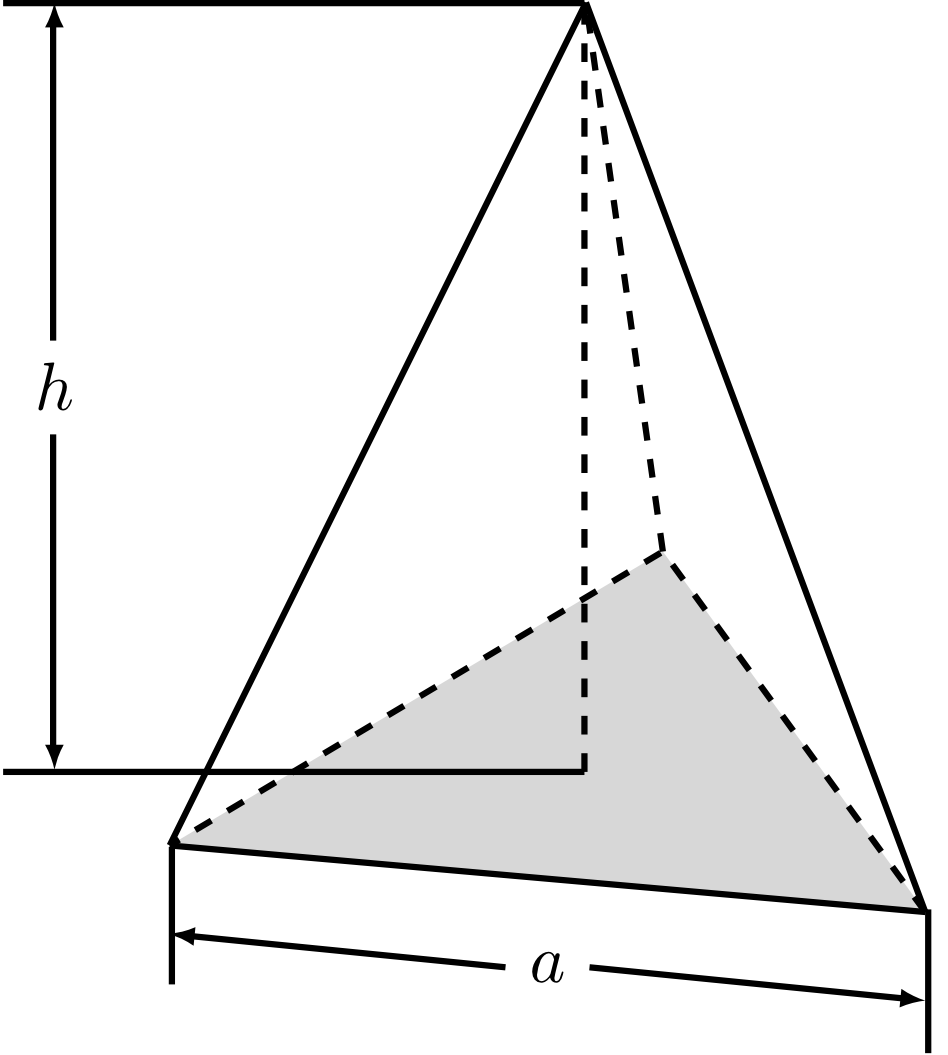
Pyramid 5.5.5

Let a polygon

G

and a point

S

with distance

h > 0

from

G

be given. A pyramid with the base

G

and the apex

S

is a solid consisting of all points lying on a line segment between

S

and a point of the base face

G

The figure above shows a pyramid with a triangular base face.
The volume

V

of the pyramid is proportional to the area of the base face

G

and the height

h

V = \frac{1}{3} \cdot G \cdot h

.
The area

O

of the surface is the sum of the area of the base face

G

and the area of the lateral surface

M

, where the area of the lateral surfaces is the sum of the areas of its triangular faces

D_{k}

(

1 \leq k \leq n

). Thus, we have

O = G + M = G + D_{1} + \dots + D_{n}

In special situations one obtains simple formulas that can be used to calculate the volume and the surface area of the solid. One example is the pyramid shown above. There, the base face is an equilateral triangle. The following exercise illustrates how to derive a formula for the surface area of a special case of a pyramid from the properties of equilateral triangles.

Exercise 5.5.6

Calculate the surface area

O

of a pyramid whose faces are all equilateral triangles with sides of length

a

.
Answer:

O

=

A pyramid whose faces are all equilateral triangles has in total four faces: a triangular base face and three further adjacent faces. Since all faces are equal, the surface area of this pyramid is given by

O = 4 \cdot F

, where

F

is the area if a single equilateral triangle. The height (altitude)

ℓ

of an equilateral triangle with sides of length

a

is, according to Pythagoras' theorem,

a^{2} = ℓ^{2} + {(\frac{a}{2})}^{2},

equal to

ℓ = \sqrt{a^{2} - \frac{1}{4} \cdot a^{2}} = \frac{1}{2} \cdot a \cdot \sqrt{3}

. Hence,

F = \frac{1}{2} \cdot a \cdot ℓ = \frac{1}{4} \cdot a^{2} \cdot \sqrt{3}

, so

O = 4 \cdot F = a^{2} \cdot \sqrt{3}

The considerations above, that a prism and a cylinder share the same constructing principle for different base faces, can be applied to the new situation of a pyramid as well. One obtains another solid if instead of a polygon (as for the case of a pyramid) a disk is now used as base face.

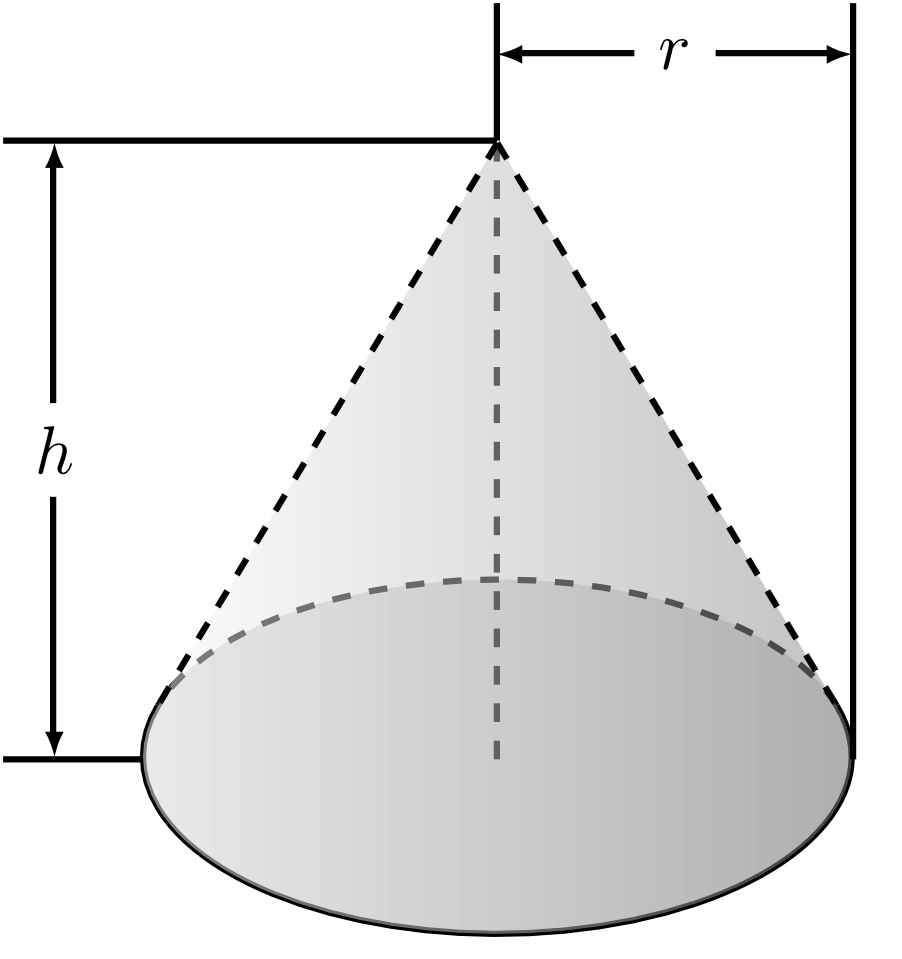
Cone 5.5.7

Let a disk

G

with radius

r

and a point

S

with distance

h > 0

from

G

be given. A cone with the base face

G

and the apex

S

is the solid consisting of all points lying on a line segment between

S

and a point of the base face

G

The volume

V

of the cone is proportional to the area of the disk

G

and its height

h

. We have

V = \frac{1}{3} \cdot G \cdot h = \frac{1}{3} \cdot π \cdot r^{2} \cdot h

.
A cone whose apex is perpendicularly above the centre of the disk is called a right circular cone.
The area of the surface of a right circular cone is the sum of the area of the disk

G

and the area of the lateral surface

M

. If

ℓ

is the distance of the apex from the boundary of the disk, then with the circumference of a circle

U = 2 π r

we have

O = G + M = π \cdot r^{2} + π \cdot r \cdot ℓ = π \cdot r \cdot (r + ℓ)

In the figure above the height

h

of the cone is given. However, the formulas given above contain the distance between the apex and the boundary of the disk. How these quantities are related?

Exercise 5.5.8

Let's imagine that the right circular cone is divided into two equal pieces by a plane trough the apex perpendicular to the base face. Then, one face of the two pieces is a triangle whose sides are defined by the height

h

, the distance

ℓ

, and the radius

r

or the diameter of the circle, respectively. Here,

r

and

h

are given.

Describe $ℓ$ as a function of $h$ and $r$ :
$ℓ$ $=$

The length of $ℓ$ is the hypotenuse of the triangle whose legs are the height $h$ of the circular cone and the radius $r$ of the disk. Form Pythagoras' theorem we have $ℓ = \sqrt{r^{2} + h^{2}}$ .
Describe the surface area $O$ of the cone as a function of $h$ and $r$ :
$O$ $=$

The result for $ℓ = \sqrt{r^{2} + h^{2}}$ obtained in the first part of the exercise is inserted in the formula for the surface area $O$ given above. Thus, we have

$O = π \cdot r \cdot (r + ℓ) = π \cdot r \cdot (r + \sqrt{r^{2} + h^{2}}) = π \cdot r^{2} \cdot (1 + \sqrt{1 + (\frac{h}{r})}) .$
The last formula shows how the relation between surface area of the cone and the area $G = π \cdot r^{2}$ of the disk depends on the ratio of the height $h$ to the radius $r$ .

Onlinebrückenkurs Mathematik

1. Elementary Arithmetic

2. Equations in one Variable

3. Inequalities in one Variable

4. System of Linear Equations

5. Geometry

6. Elementary Functions

7. Differential Calculus

8. Integral Calculus

9. Objects in the Two-Dimensional Coordinate System

10. Basic Concepts of Descriptive Vector Geometry

11. Language of Descriptive Statistics

Chapter 5 Geometry

5.5.2 Simple Geometric Solids

Example 5.5.1

Prism 5.5.2

Cylinder 5.5.3

Sphere 5.5.4

Pyramid 5.5.5

Exercise 5.5.6

Cone 5.5.7

Exercise 5.5.8