Chapter 5 Geometry

Section 5.1 Elements of Plane Geometry

5.1.3 Intercept Theorems


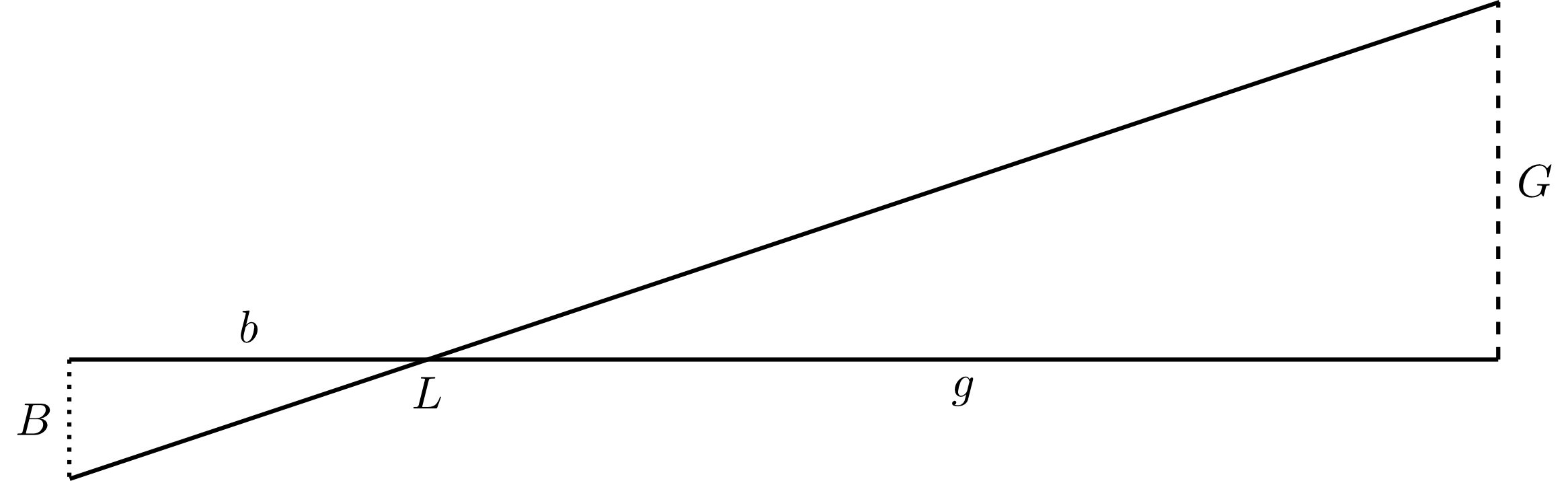
A pinhole camera provides a small image of the outside space. The ratio of the size of the image B to the size of the object G equals the ratio of the distance b from the pinhole L to the distance g from L:

B G = b g  .



Properties of images arising from uniform scaling can also be described by means of the intercept theorems (see also Figure 5.3.17).
What all examples applying the intercept theorems have in common is that rays (or lines) with an intersection point are intersected by parallel lines.
Intercept Theorems 5.1.4

Let S be the common initial point of the two rays s1 and s2 proceeding through the points A and C, respectively. The point B is on the ray s1 and the point D is on the ray s2 . First, we consider the line segments between the points on the two rays and then the line segments between the rays.
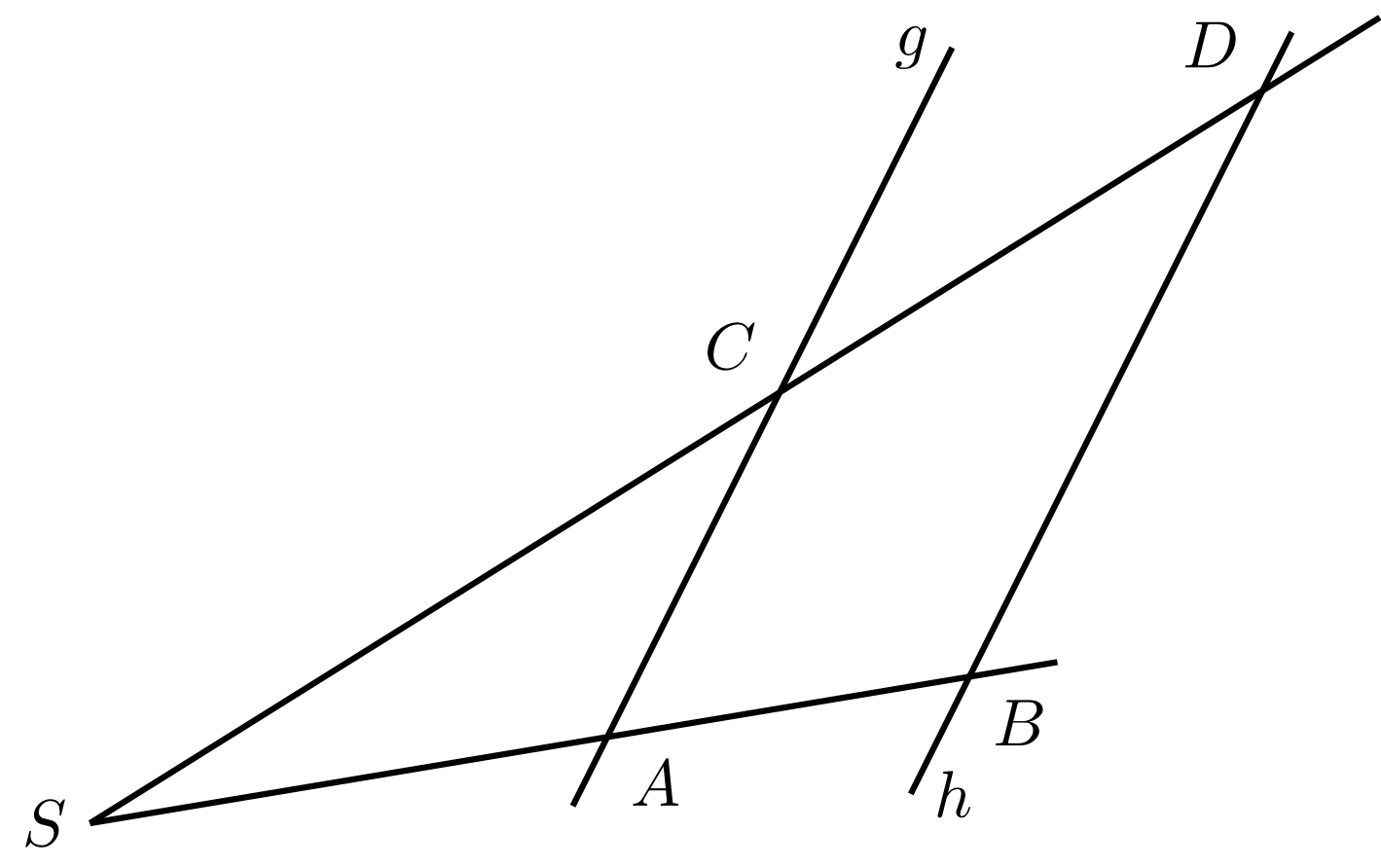For two points P and Q, PQ ‾ is the line segment from P to Q and [ PQ ‾ ] denotes the length of this line segment.






If the lines g and h are parallel, the following statements hold:
  • The ratio of the line segments on one of the two rays equals the corresponding ratio of the line segments on the other:

    [ SA ‾ ] [ SC ‾ ] = [ AB ‾ ] [ CD ‾ ] = [ SB ‾ ] [ SD ‾ ]  .

    This can also be expressed in the form:

    [ SA ‾ ] [ AB ‾ ] = [ SC ‾ ] [ CD ‾ ]     and     [ SA ‾ ] [ SB ‾ ] = [ SC ‾ ] [ SD ‾ ]  .


  • The ratio of the line segments on the parallel lines equals the ratio of the corresponding line segments starting from S on a single ray

    [ SA ‾ ] [ SB ‾ ] = [ AC ‾ ] [ BD ‾ ] = [ SC ‾ ] [ SD ‾ ]  .

    This can also be expressed in the form:

    [ SA ‾ ] [ AC ‾ ] = [ SB ‾ ] [ BD ‾ ]     and     [ SC ‾ ] [ CA ‾ ] = [ SD ‾ ] [ DB ‾ ]  ,

    where [ AC ‾ ]=[ CA ‾ ] and [ BD ‾ ]=[ DB ‾ ].

The statements of the intercept theorems also hold if two lines intersecting in a point S are considered instead of the two rays. An application example of this case is the pinhole camera mentioned above.
In this way, distances between points can be calculated without measuring the length of the line segments directly.
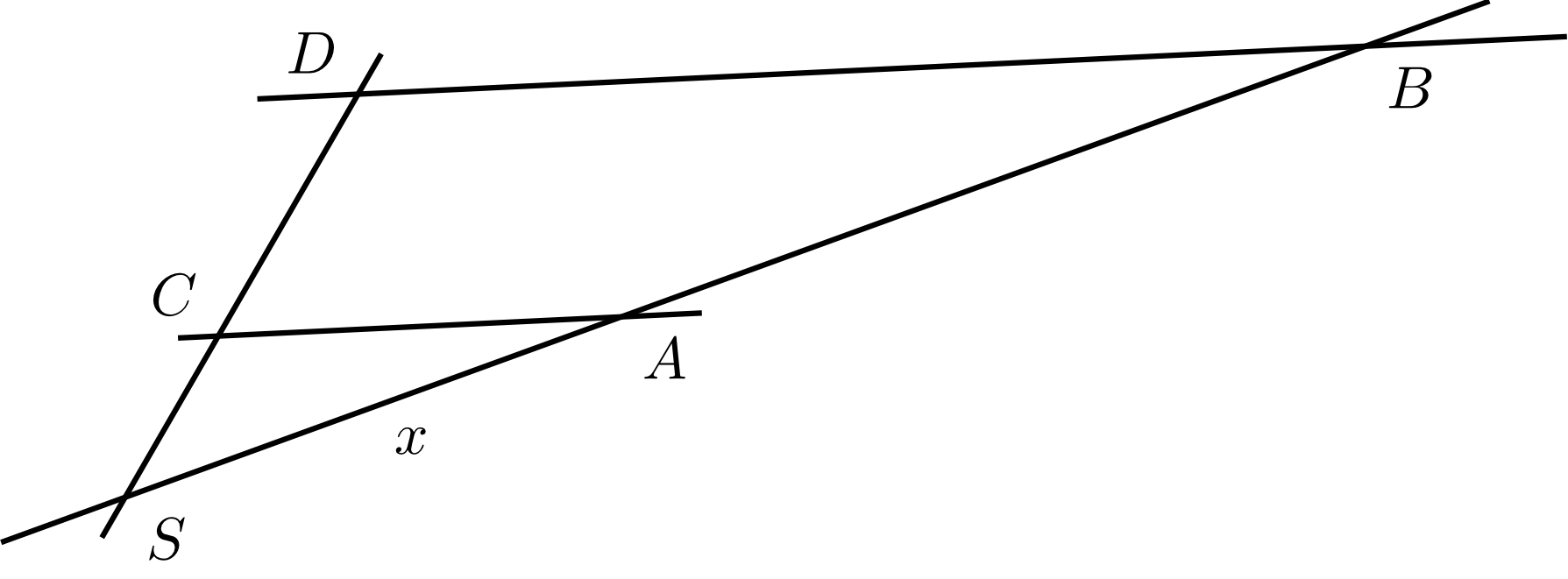
Example 5.1.5
Let four points A, B, C, and D be given. These points define the two lines AB and CD intersecting at the point S. Furthermore, it is known that the lines AC and BD are parallel. Between the points the following distances were measured: [ AB ‾ ]=51, [ SC ‾ ]=12, and [ CD ‾ ]=18.

From this, the distance between A and S can be calculated. Let x denote the required distance. Then, according to the intercept theorems, we have

x [ AB ‾ ] = [ SC ‾ ] [ CD ‾ ]  ,

from which

x= [ SC ‾ ] [ CD ‾ ] ·[ AB ‾ ]= 12 18 ·51= 2 3 ·51=34

follows.

: