Chapter 5 Geometry
Section 5.4 Polygons, Area and Circumference5.4.5 Area
The area of a surface equals the number of unit squares required to cover this surface completely.
|
|
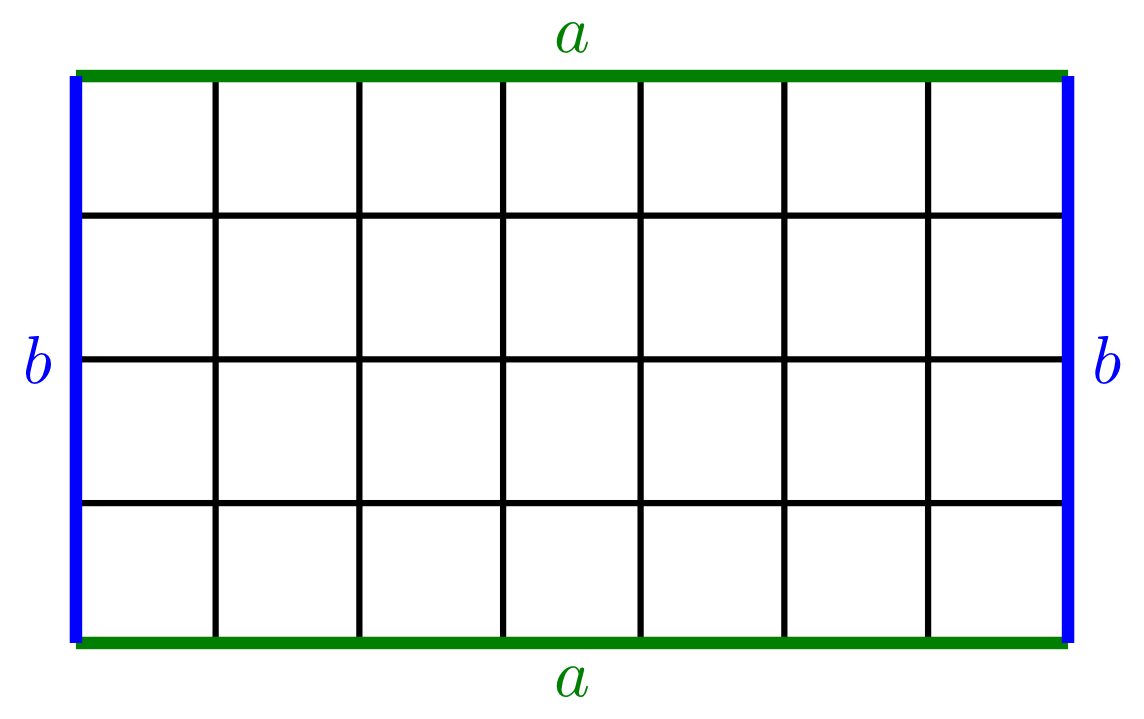
Area of a Rectangle 5.4.10
The area of a rectangle with sides of lengths and is
And how is the area calculated if the triangle is not right-angled?
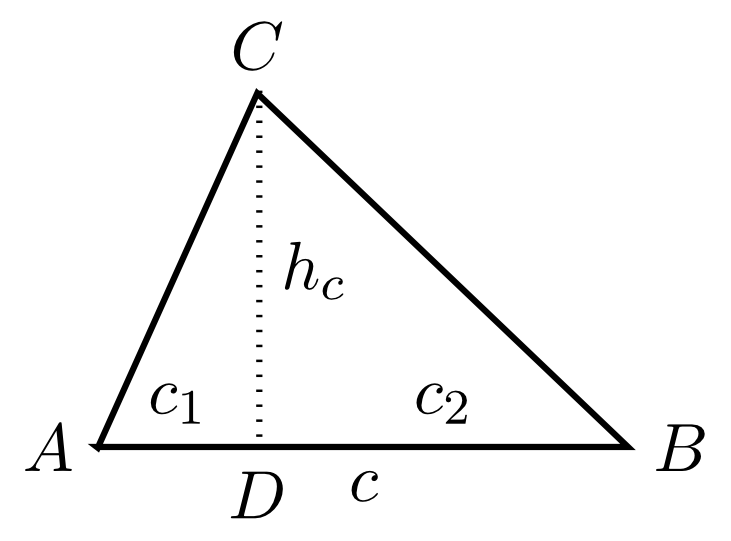
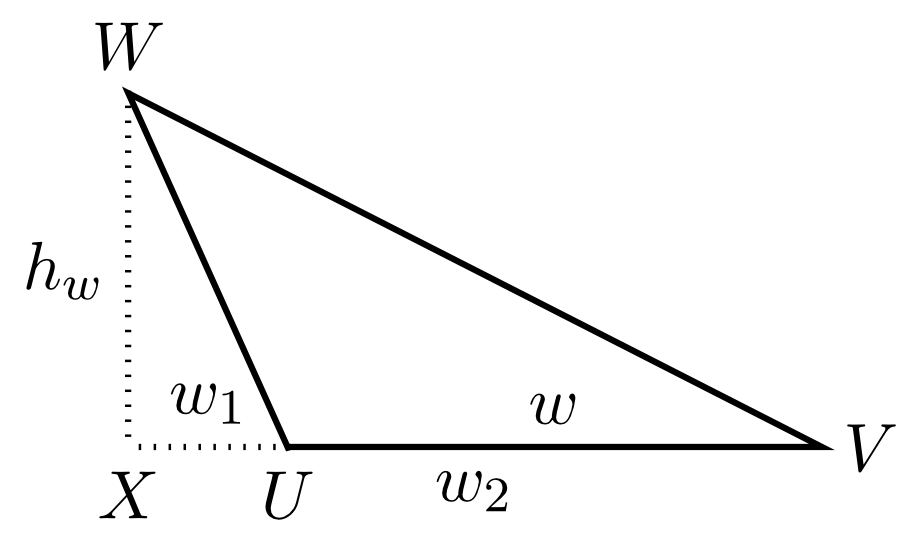
Every triangle can be divided into two right triangles by drawing a line from one vertex to the opposite side such that this line is perpendicular to the side. This line is called the altitude of a triangle on a specific side , where is the index of the side , , or .
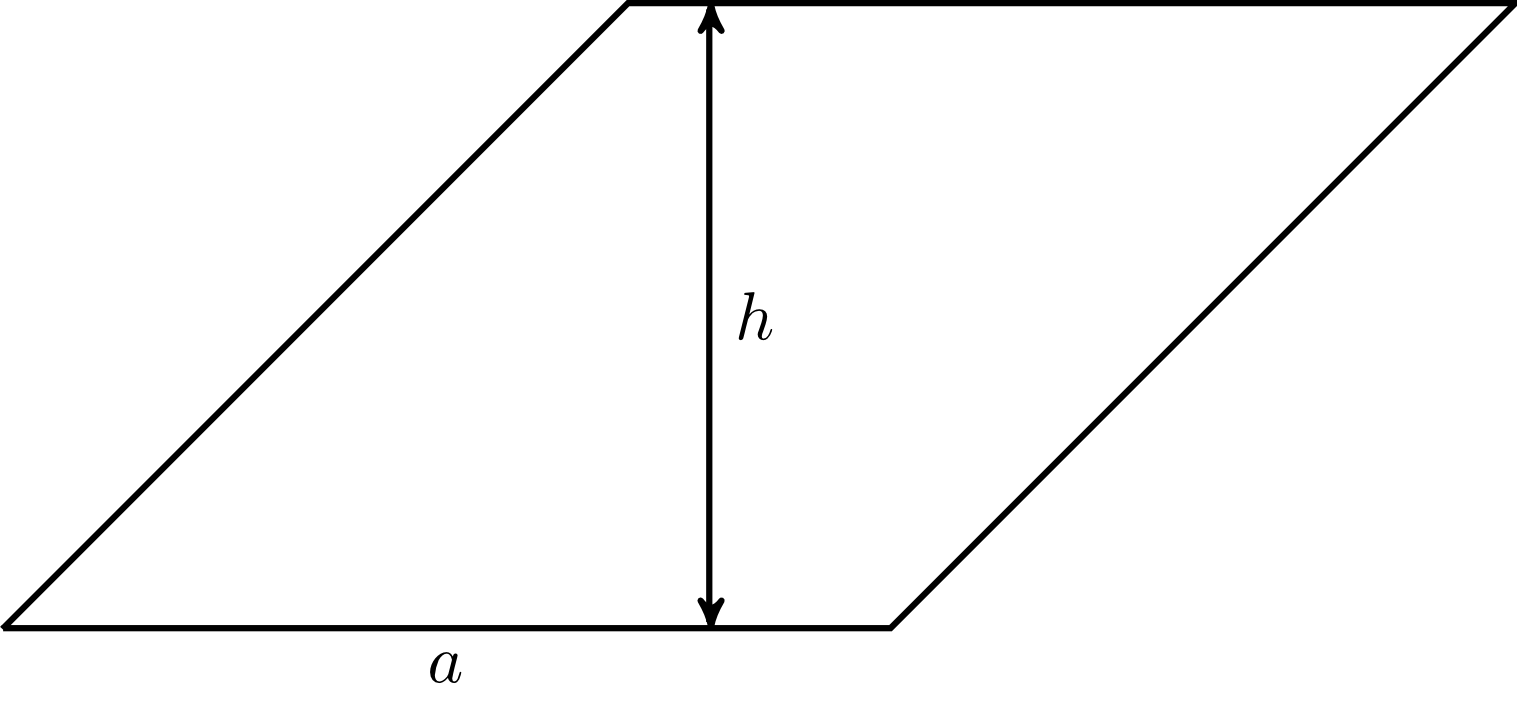
Depending on whether the new line is interior or exterior to the triangle, the area of the triangle equals the sum or the difference of the areas of the two resulting right triangles:
Thus, on the left, we have (if is the area of the triangle )
On the right, we have
Thus the area can always be calculated from the length of one side and the length of the altitude perpendicular to the corresponding side.
Area of a Triangle 5.4.11
The area of a triangle equals half the product of the length of a side and the length of the corresponding altitude of the triangle:
Here, the altitude of a triangle on a side denotes the line segment from the vertex opposite the side to the line containing the side itself, perpendicular to this side.
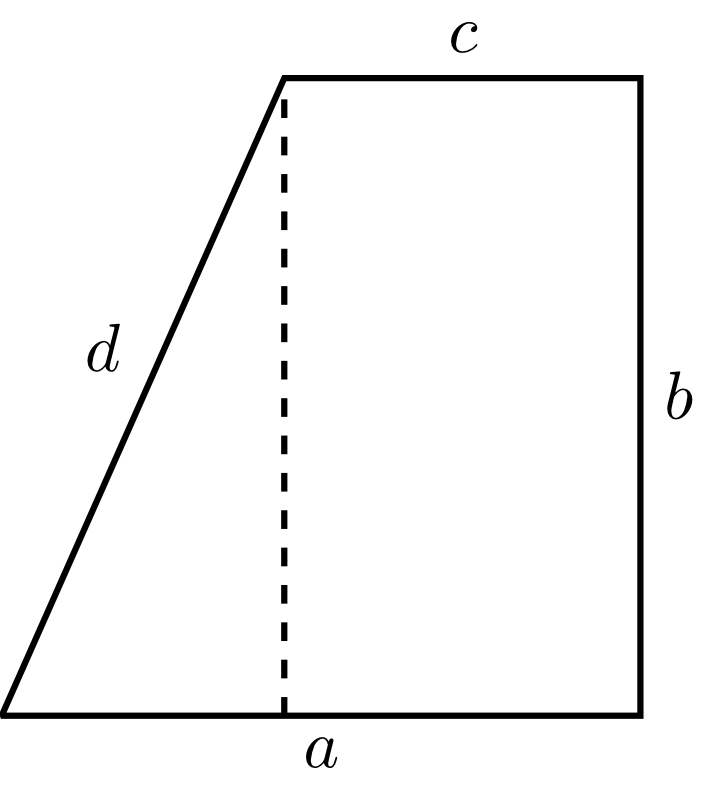
Using the formula for the area of triangles, areas of polygons can also be calculated. This is due to the fact that every polygon can be divided into triangles by adding diagonals to the polygon until all subareas are triangles. However, the considerations will remain restricted here to a few simple shapes. In the following example, the polygon can be divided into a triangle and a rectangle. As a result, the calculation will be particularly easy.
Finally, we will calculate the area of a circle. Info Box 5.2.6 introduced the number describing the ratio of the circumference of a circle to its radius. The formula for the area of the circle also involves .
Area of a Circle 5.4.16
The area of a circle with radius is
Example 5.4.17
Let the area of a circle with radius be . This fact can be used to calculate an approximate value of the number : We have , hence . Inserting the given values results in the approximate value
 Onlinebrückenkurs Mathematik
Onlinebrückenkurs Mathematik