Chapter 6 Elementary Functions

Section 6.1 Basics of Functions

6.1.2 Assignments between Sets

We start with a first example of a function as an assignment between two sets. For this purpose, we consider the set of natural numbers $\mathbb{N}$ and the set of rational numbers $\mathbb{Q}$, and visualise these two sets as two "containers" filled with numbers.

Now, we want to create an assignment between the elements of these two sets as follows. To every number $n\in \mathbb{N}$ half of this number $\frac{n}{2}\in \mathbb{Q}$ is assigned, i.e. to the number $1\in \mathbb{N}$ we assign the number $\frac{1}{2}\in \mathbb{Q}$, to the number $2\in \mathbb{N}$ we assign the number $1\in \mathbb{Q}$, etc. In the figure below, this is illustrated by arrows that indicate which numbers in $\mathbb{Q}$ are assigned to which numbers in $\mathbb{N}$.

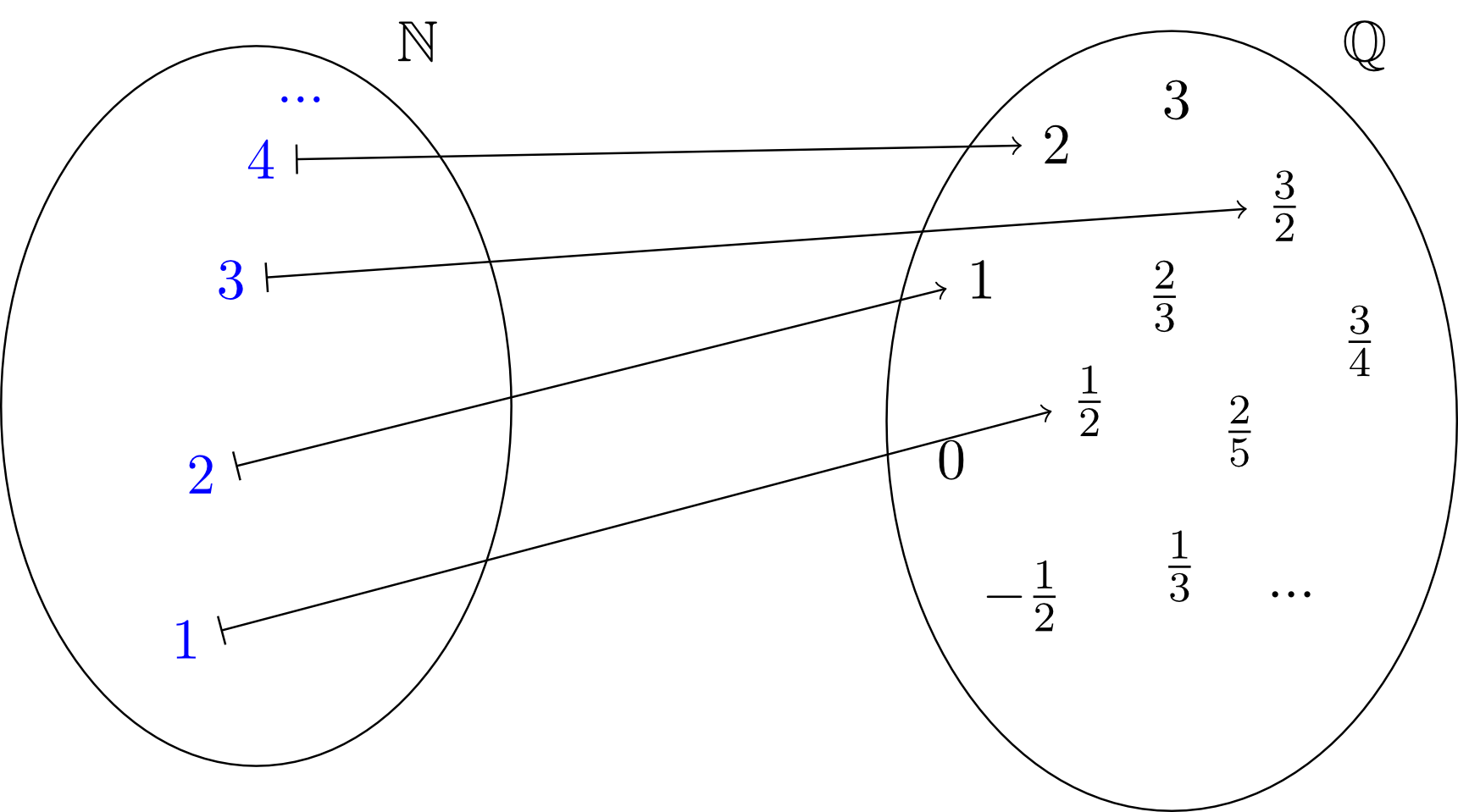
For the assignment of single elements of the sets, described above in words, we use the so-called assignment arrow. This is an arrow that has a bar at its tail: $⟼$. It says that to the number on the side with the bar the number on the side with the arrow is assigned:

${\displaystyle \mathbb{N}\ni 1⟼0.5\in \mathbb{Q}\hspace{0.5em},\hspace{0.5em}\hspace{0.5em}\mathbb{N}\ni 2⟼1\in \mathbb{Q}\hspace{0.5em},\hspace{0.5em}\hspace{0.5em}\text{etc.}}$
With these assignments, we have now constructed a function from the natural numbers $\mathbb{N}$ to the rational numbers $\mathbb{Q}$. In mathematics, this assignment is named, i.e. a symbol is allocated (often this is $f$ for function), that shall describe exactly this assignment. For this purpose, the sets of numbers from which and to which the assignment will be done must be noted. In our case, to the elements of the set of natural numbers $\mathbb{N}$ the rational numbers are assigned. Mathematically, this is expressed by a so-called mapping arrow $\to$, i.e. an arrow that has the target set at its head and the set, whose elements are assigned to, at its tail. Thus, in our case we have

${\displaystyle f:\mathbb{N}\to \mathbb{Q}\hspace{0.5em}.}$
This reads as "the function $f$ maps $\mathbb{N}$ to $\mathbb{Q}$".
Furthermore, we can now ask whether the assignments of this function, $1⟼\frac{1}{2},\hspace{0.5em}2⟼1,\hspace{0.5em}\text{etc.}$, can be described in a more compact way. To do this, we recall the beginning of this example. We decided to assign to every natural number $n$ its half $\frac{n}{2}$. So we can write this arbitrary natural number $n$ and the corresponding rational number $\frac{n}{2}$ left and right to the assignment arrow, respectively:

${\displaystyle n⟼\frac{n}{2}\hspace{0.5em}.}$
This reads as "$n$ is mapped to $\frac{n}{2}$". This notation is also called mapping rule of the function. Another notation for the mapping rule uses the name of the function:

${\displaystyle f(n)=\frac{n}{2}\hspace{0.5em}.}$
This reads as "$f$ of $n$ equals $\frac{n}{2}$". Altogether we can describe this function $f$ as follows:

${\displaystyle f:\mathrm{\hspace{0.5em}\hspace{0.5em}}\{\begin{array}{ccc}\hfill \mathbb{N}& \hfill \to \hfill & \mathbb{Q}\hfill \\ \hfill n& \hfill ⟼\hfill & \frac{n}{2}\hspace{0.5em}.\hfill \end{array}}$
Finally, this reads as "the function $f$ maps $\mathbb{N}$ to $\mathbb{Q}$, each $n\in \mathbb{N}$ is mapped to $\frac{n}{2}\in \mathbb{Q}$". Throughout this module, we will continue to use this summarising notation of functions.
Let us consider a few further simple examples for functions.


The examples above show some basic properties of functions for which we will now introduce specific terminology.

If we consider the mapping rule $h(x)=\frac{1}{x}$ of the function, we see that there is no reason not to insert in $\frac{1}{x}$ any real number $x$, excluding the value $x=0$, since the operation "$\frac{1}{0}$" has no solution. Therefore, in specifying the domain, we can distinguish between numbers that are excluded because they are not allowed to be inserted in the mapping rule at all and those that are excluded because the function is just defined accordingly. This now leads to the term of the maximal domain of a function, i.e. the maximum subset of real numbers $ℝ$ that can be used as the domain of a function with a known mapping rule.


For the definition of a function, a second set (beside the domain) is required, the set that is the target of the assignment by the function. This set is called target set or codomain. Let us again consider the function

${\displaystyle \phi :\mathrm{\hspace{0.5em}\hspace{0.5em}}\{\begin{array}{ccc}\hfill (0;1)& \hfill \to \hfill & ℝ\hfill \\ \hfill y& \hfill ⟼\hfill & 3y+1\hfill \end{array}}$
in Example 6.1.4. Its target set is the set of real numbers $ℝ$. The target set of the function

${\displaystyle f:\mathrm{\hspace{0.5em}\hspace{0.5em}}\{\begin{array}{ccc}\hfill \mathbb{N}& \hfill \to \hfill & \mathbb{Q}\hfill \\ \hfill n& \hfill ⟼\hfill & \frac{n}{2}\hfill \end{array}}$
in the first example of this section is the set of rational numbers $\mathbb{Q}$. Here, we see an important difference between the domain and target set of a function. The domain contains all numbers, and only those numbers, that are allowed to be inserted (and one wishes to insert) in the mapping rule of the function. However, the target set can contain all numbers that can potentially appear as a result of the mapping function.
In this context the question arises: What is the smallest target set that can be used for a function with given domain and known mapping rule? The smallest target set is the set of numbers that - for a given domain and mapping rule - indeed appear as targets of the assignment. This set is called range or image, and its elements are called values of the function. For a function $f$, the symbol $W_f$ is used for the image. For the values of a function $f$ of an independent variable $x$ we write generally $f(x)\in W_f$, as in the mapping rule, or we introduce another variable, e.g. $y=f(x)\in W_f$.

Such tables of values are useful to get an overview of the values of a function. However, from a mathematical point of view, they are not sufficient to be completely sure what the actual range of a function is. One method to determine the range of a function is based on solving inequalities: