Chapter 6 Elementary Functions
Section 6.2 Linear Functions and Polynomials6.2.9 Rational Functions
A general rational function has a mapping rule that is the quotient of two polynomials. Some examples with their graphs are given below. Of course, for these functions numbers for which the denominator in the mapping rule equals zero must also be excluded from the domain.Exercise 6.2.16
For the function
find the maximum domain of .
find the maximum domain of .
Exercise 6.2.17
For the rational functions in Example 6.2.15, specify the degree of the polynomials in the numerator and the denominator and find their roots.
The roots of a rational function are the roots of the numerator. For example, the function
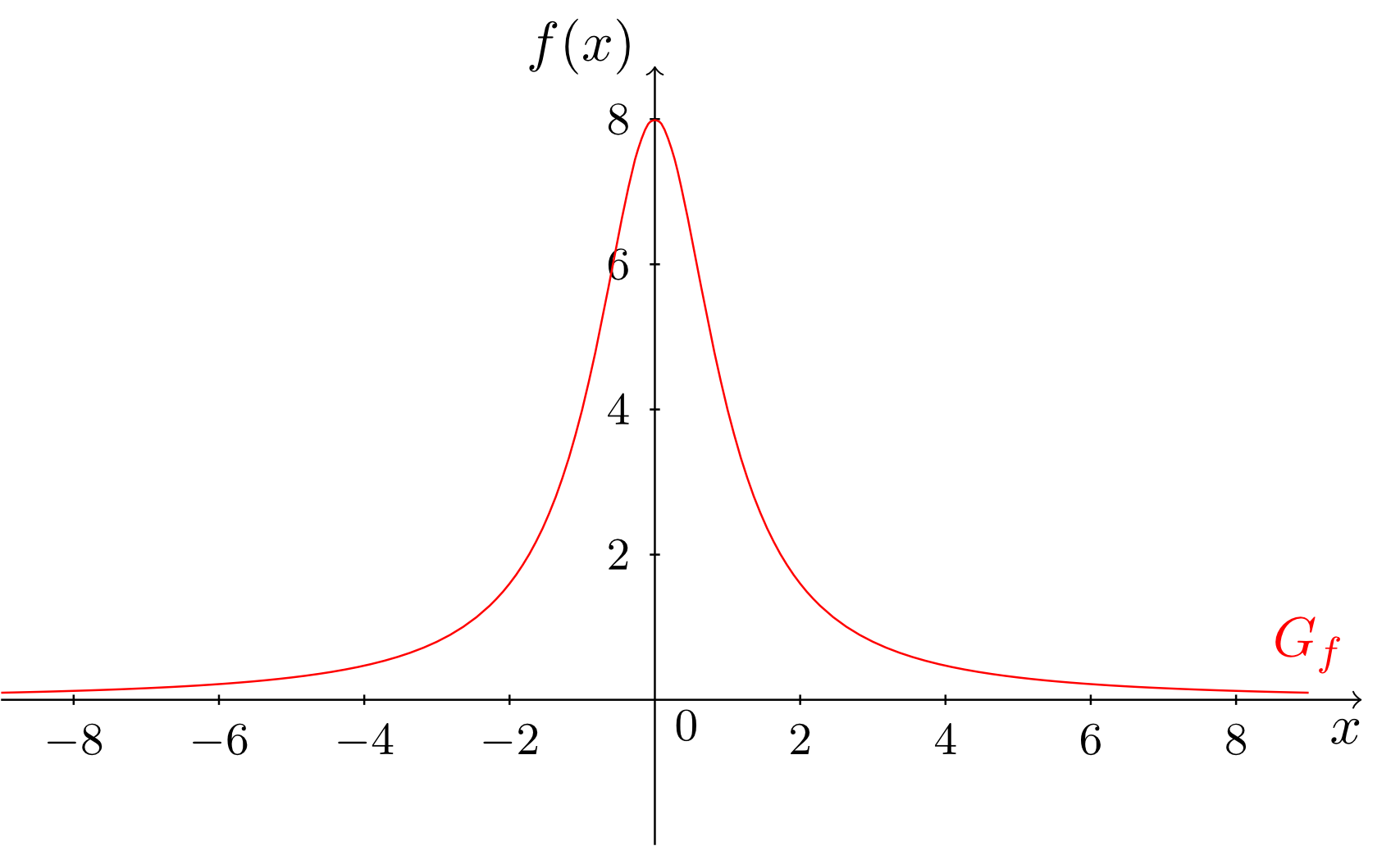
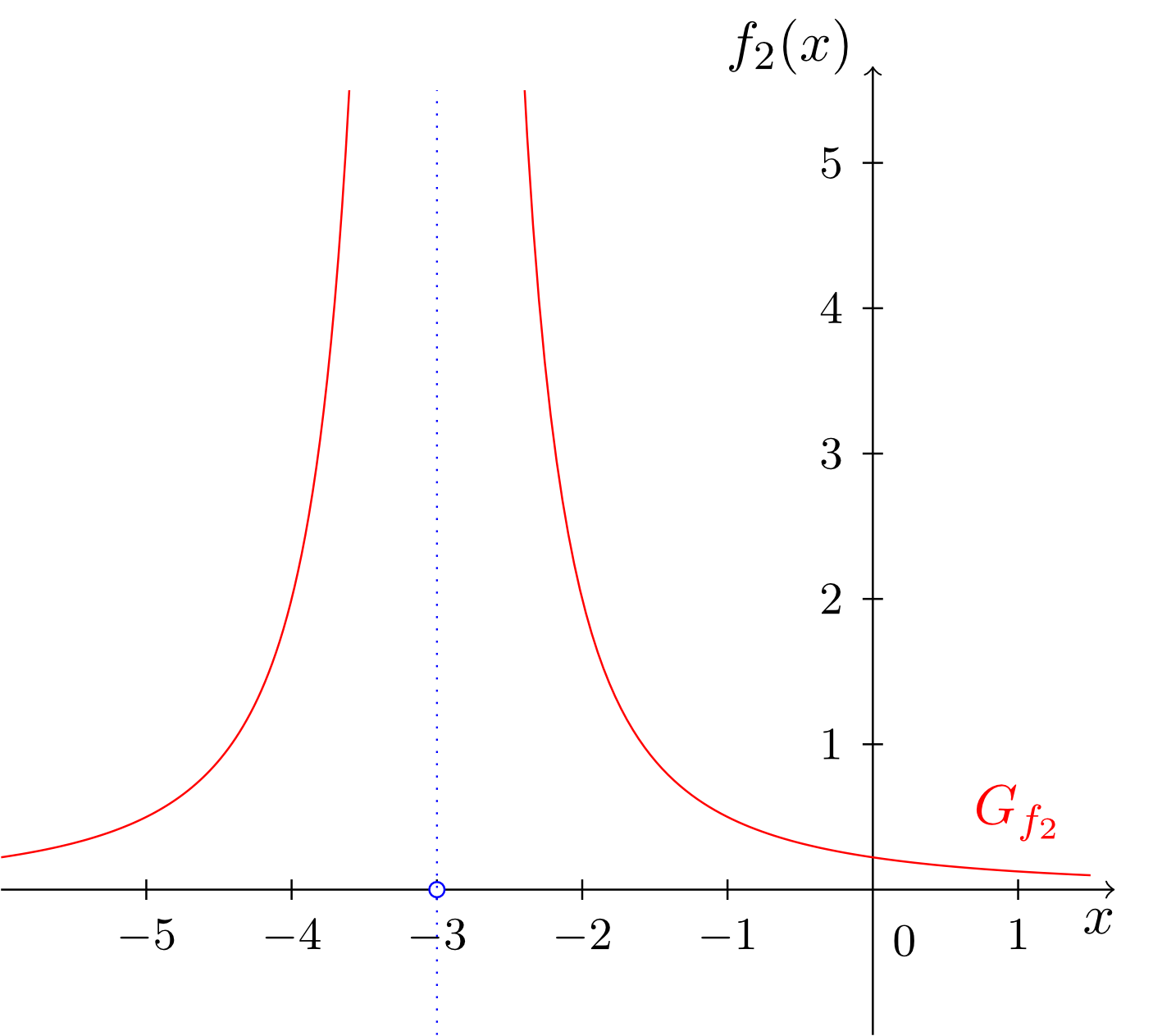
has a single root at . The roots of the denominator of rational functions that must be excluded from the domain often have to be investigated further. It is of particular interest how the graphs of functions behave in the neighbourhood of gaps in the domain. The roots of the denominator are also called poles. The next examples will illustrate the different types of poles that can occur.
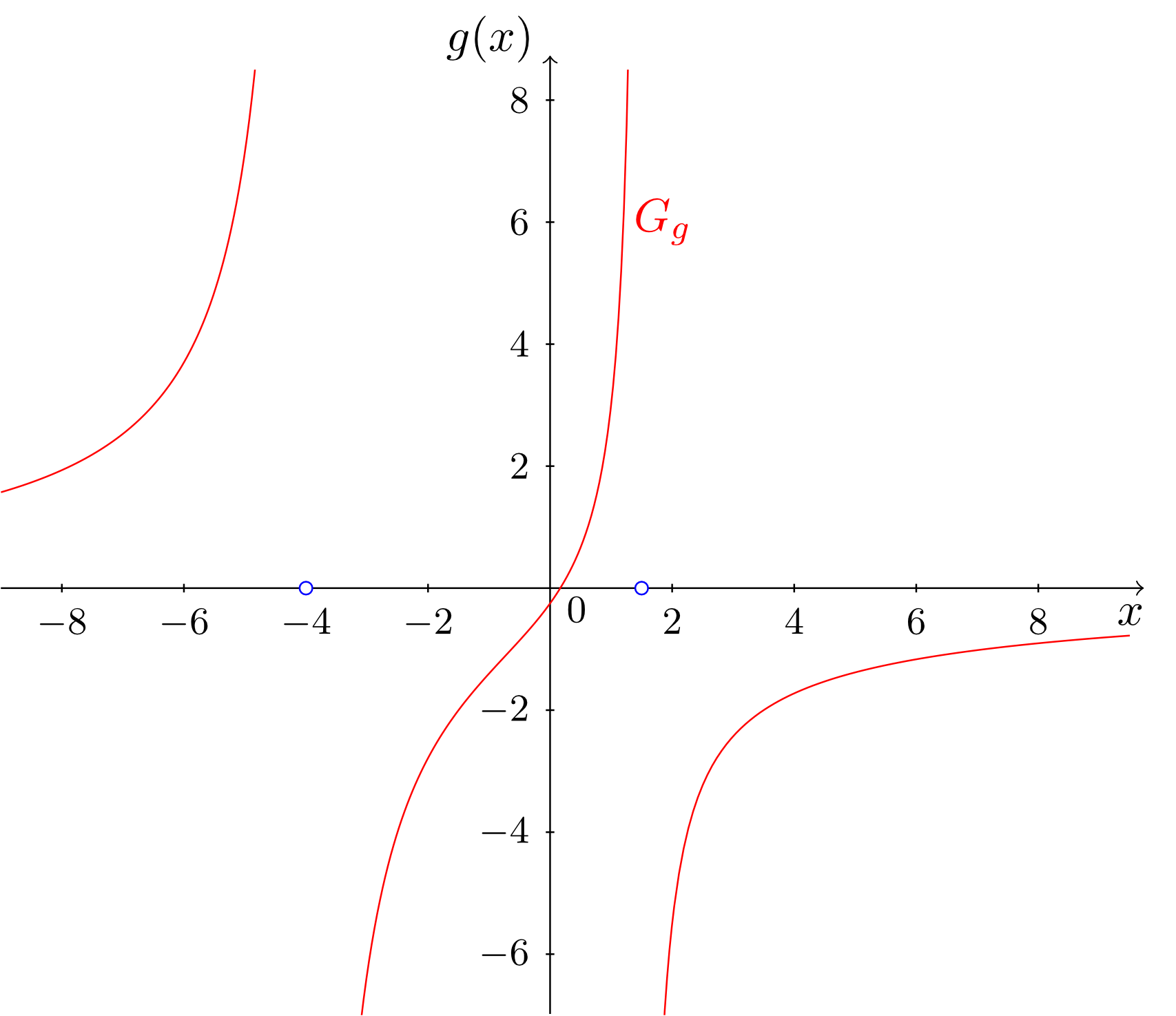
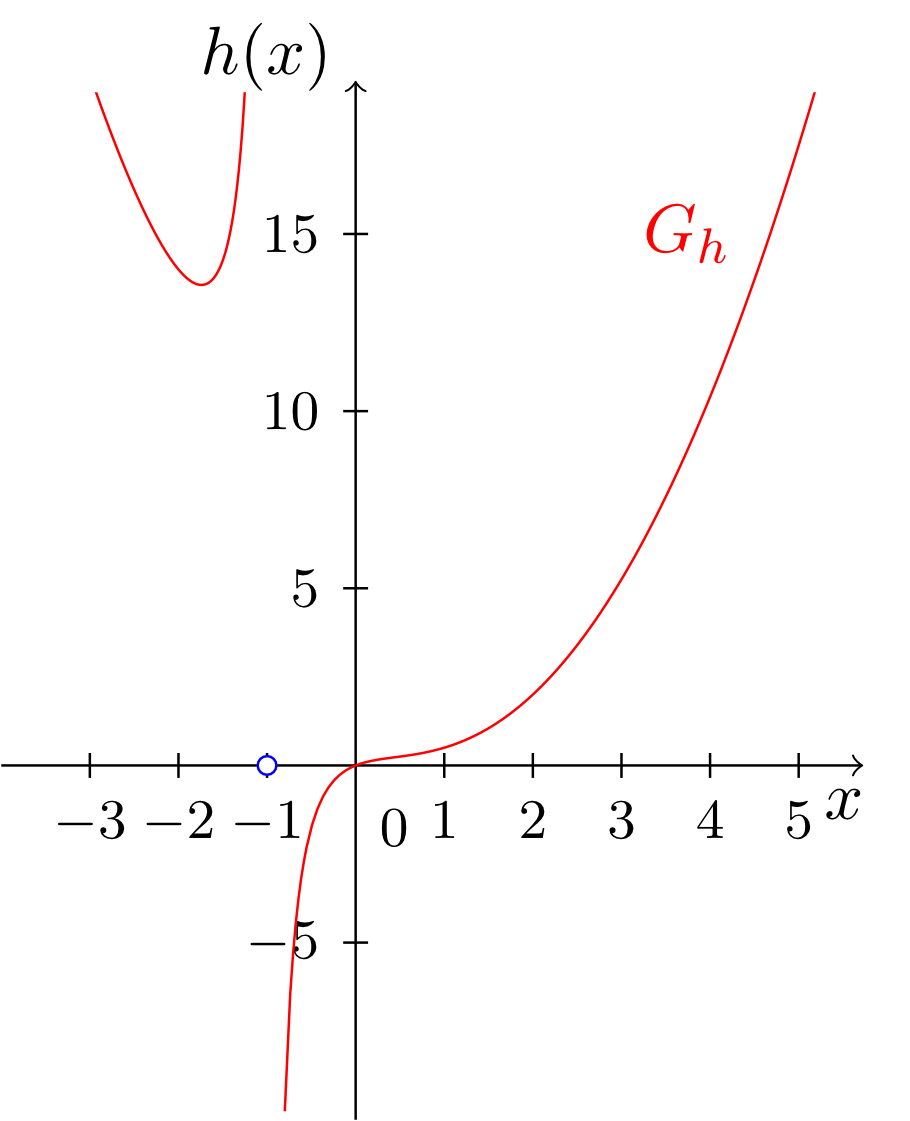
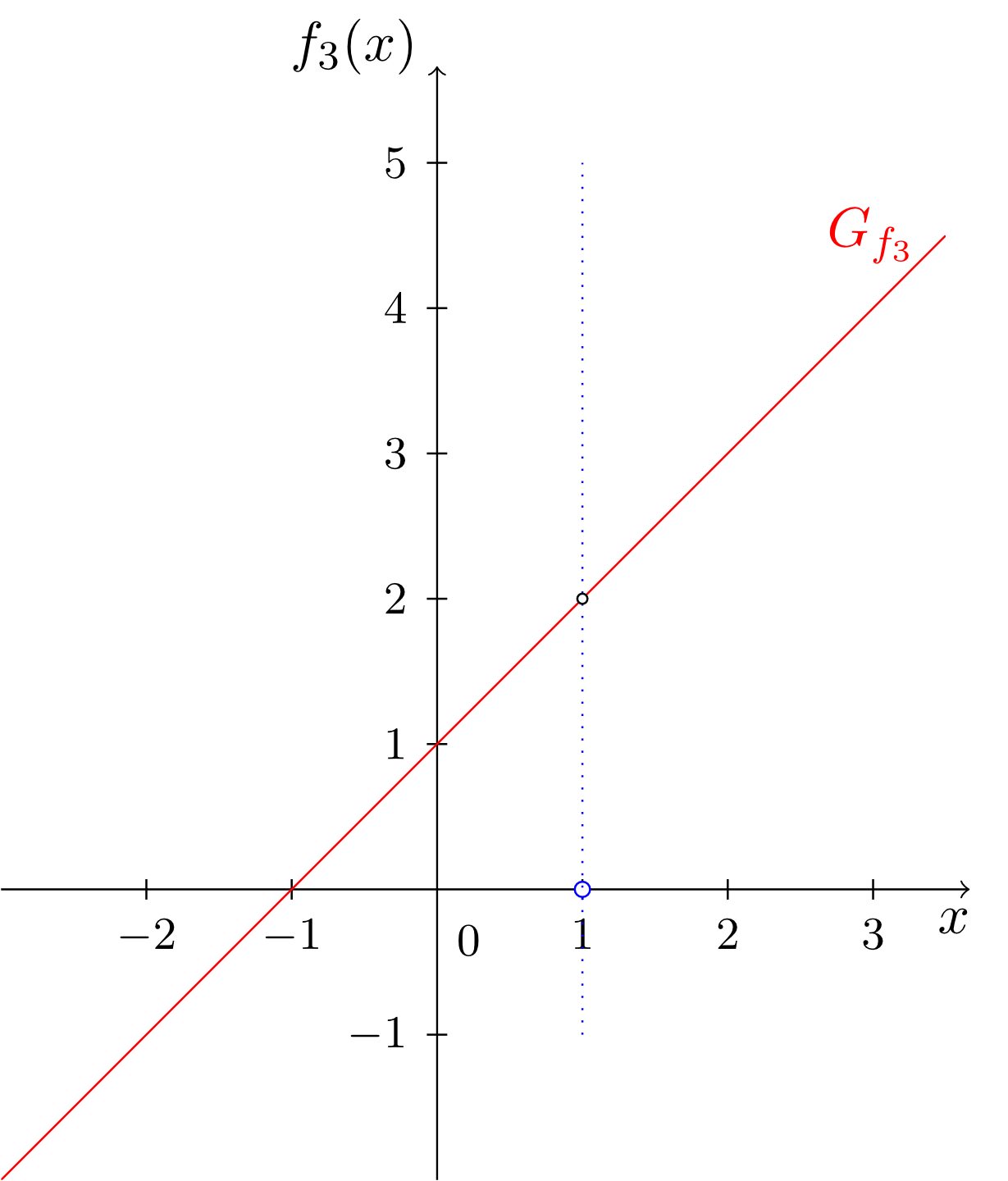
At and the functions and , respectively, have so-called (proper) poles, and at the function has a so-called removable singularity. Looking at the graphs, the difference between these types of poles becomes clear. For (proper) poles, the graph rises or falls unboundedly in the neighbourhood of the pole, and for removable singularities the graph ends left and right in the "gap".
In the mapping rules of the three functions, this difference is expressed as follows: the values and are roots of the denominator, but they are not roots of the numerator of the functions and , respectively. Actually, the functions and do not have any roots in the numerator. In such cases, the roots of the denominator are always (proper) poles.
Exercise 6.2.19
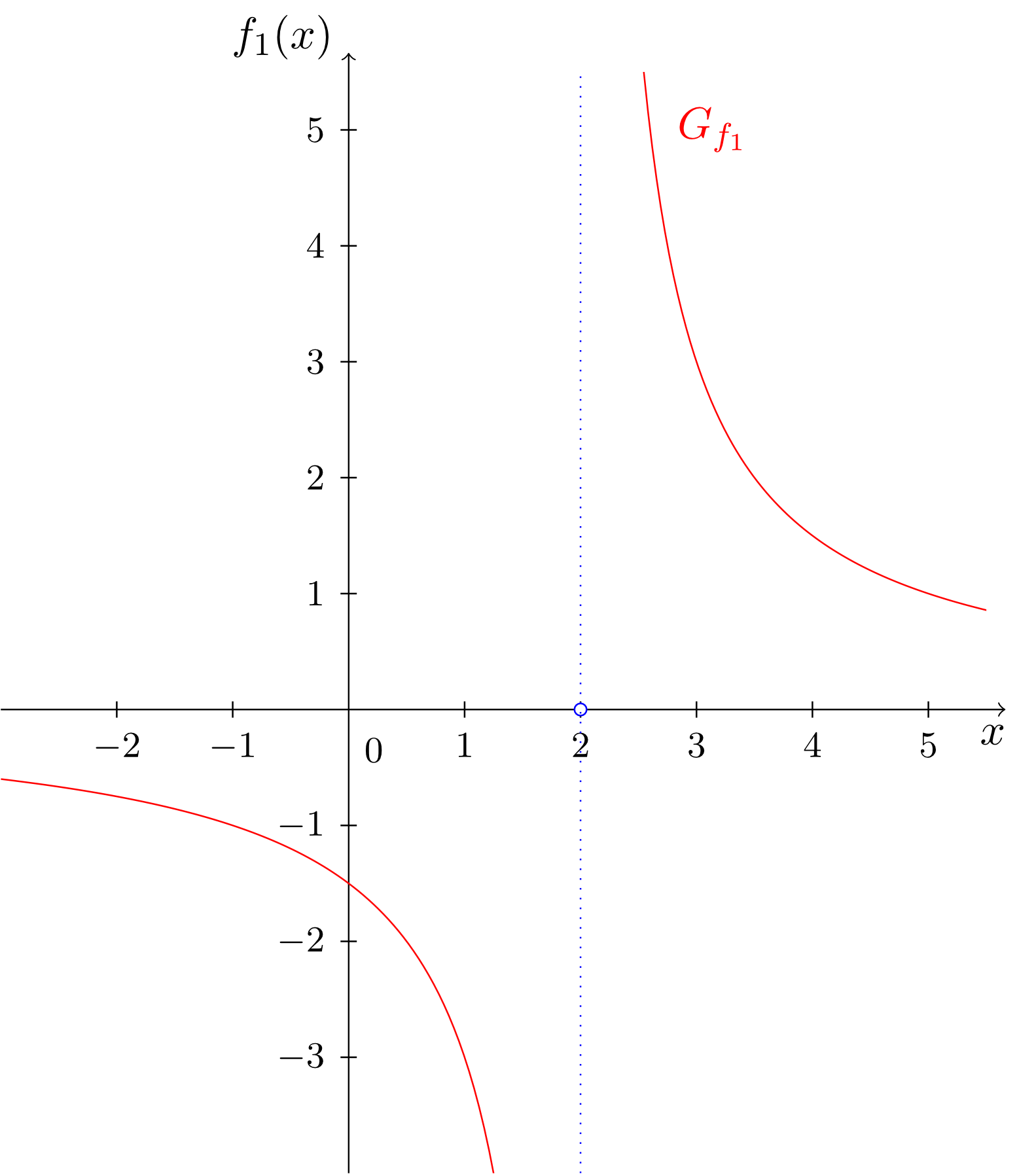
Is the denominator's root of the function
a proper pole? If so, give reasons for your answer.
a proper pole? If so, give reasons for your answer.
Between the two poles of and there is a further difference. At the pole of , the function has a change of sign. The graph of falls left to the pole unboundedly to minus infinity and rises right to the pole (coming from the right) unboundedly to plus infinity.
The graph of rises on both sides of the pole at (while approaching the pole) unboundedly to plus infinity, and hence, there is no change of sign in the function values.
However, in the mapping rule of , the term responsible for the pole at can be cancelled out. For rational functions that have a removable singularity, this is always possible.
Exercise 6.2.20
Find all poles/singularities of the function
and determine their type. Specify the maximum domain of the function.
and determine their type. Specify the maximum domain of the function.
 Onlinebrückenkurs Mathematik
Onlinebrückenkurs Mathematik