Chapter 6 Elementary Functions

Section 6.2 Linear Functions and Polynomials

6.2.8 Hyperbolas

We consider functions which have a reciprocal relation in their mapping rule. For the determination of the maximum domain of such a function, note that the denominator must be non-zero.
A few examples of reciprocal functions are listed below; these are reciprocals of monomials, and they are also called functions of hyperbolic type.

${\displaystyle f_1:\mathrm{\hspace{0.5em}\hspace{0.5em}}\{\begin{array}{ccc}\hfill ℝ\setminus \{0\}& \hfill \to \hfill & ℝ\hfill \\ \hfill x& \hfill ⟼\hfill & \frac{1}{x}\hspace{0.5em},\hfill \end{array}}$


${\displaystyle f_2:\mathrm{\hspace{0.5em}\hspace{0.5em}}\{\begin{array}{ccc}\hfill ℝ\setminus \{0\}& \hfill \to \hfill & ℝ\hfill \\ \hfill x& \hfill ⟼\hfill & \frac{1}{x^2}\hspace{0.5em},\hfill \end{array}}$


${\displaystyle f_3:\mathrm{\hspace{0.5em}\hspace{0.5em}}\{\begin{array}{ccc}\hfill ℝ\setminus \{0\}& \hfill \to \hfill & ℝ\hfill \\ \hfill x& \hfill ⟼\hfill & \frac{1}{x^3}\hspace{0.5em},\hfill \end{array}}$
etc. Their graphs are as follows.

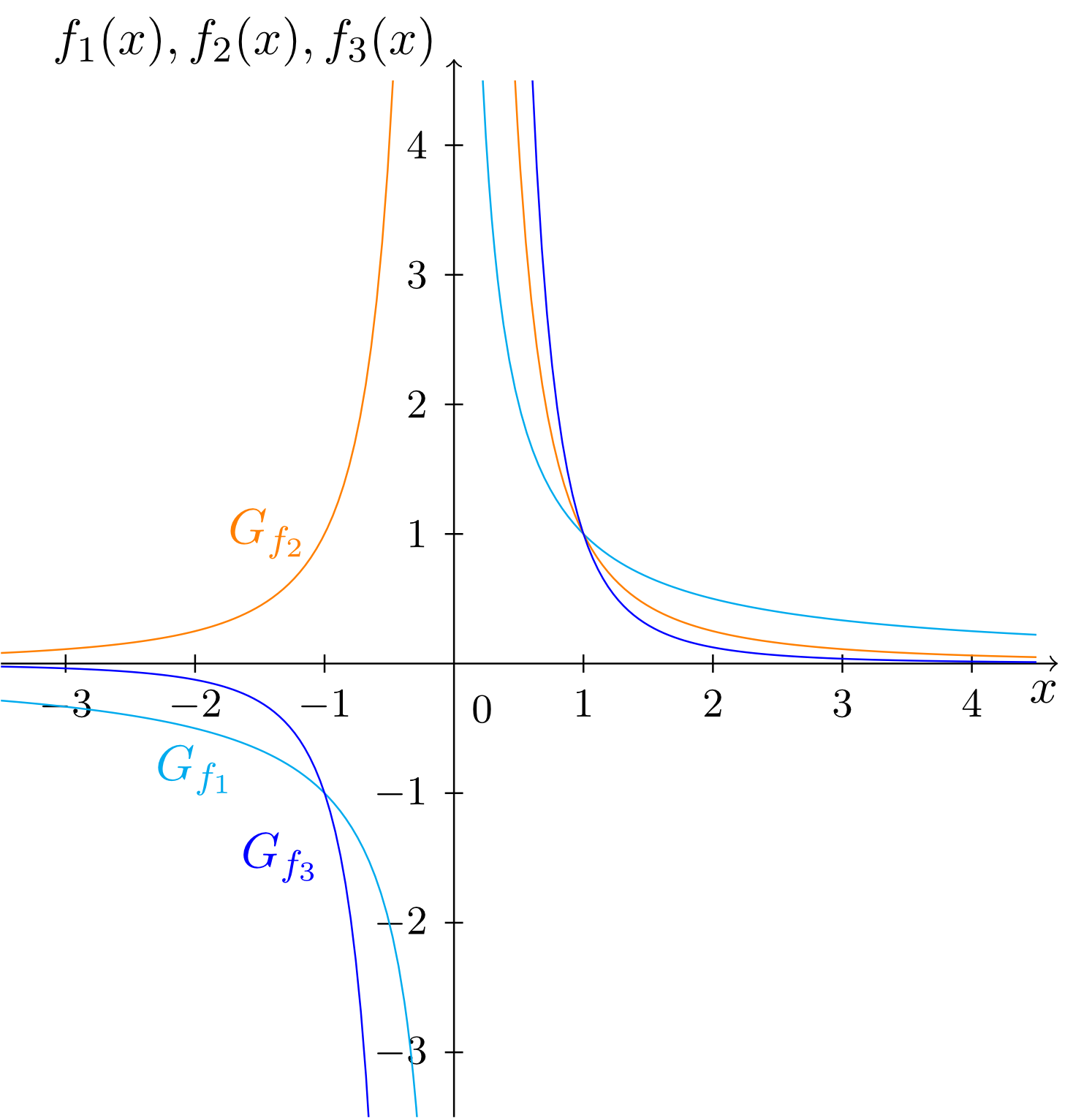
In particular, the graph of the function

${\displaystyle f_1:\mathrm{\hspace{0.5em}\hspace{0.5em}}\{\begin{array}{ccc}\hfill ℝ\setminus \{0\}& \hfill \to \hfill & ℝ\hfill \\ \hfill x& \hfill ⟼\hfill & \frac{1}{x}\hfill \end{array}}$
is called the hyperbola.
Generally, for the reciprocal of an arbitrary monomial of degree $n\in \mathbb{N}$ a corresponding function of hyperbolic type can be specified.

${\displaystyle f_n:\mathrm{\hspace{0.5em}\hspace{0.5em}}\{\begin{array}{ccc}\hfill ℝ\setminus \{0\}& \hfill \to \hfill & ℝ\hfill \\ \hfill x& \hfill ⟼\hfill & \frac{1}{x^n}\hspace{0.5em}.\hfill \end{array}}$

Further examples for functions of hyperbolic type were already considered in Example 6.1.12 and in Exercise 6.1.13 in Section 6.1.3.