Chapter 6 Elementary Functions

Section 6.4 Exponential and Logarithmic Functions

6.4.4 Logarithmic Function

In Section 6.4.3 we studied the natural exponential function

${\displaystyle g:\mathrm{\hspace{0.5em}\hspace{0.5em}}\{\begin{array}{ccc}\hfill ℝ& \hfill \to \hfill & (0;\infty )\hfill \\ \hfill x& \hfill ⟼\hfill & g(x)=e{}^x\hfill \end{array}}$


In particular, we pointed out a very important property of the natural exponential function: it is strictly increasing. If the graph of this function is reflected about the angle bisector between the first and the third quadrant (see Chapter 9), one obtains the graph of the natural logarithmic function that has the symbol $\ln$:

Here, the equation shall be read in such a way that $\ln (x)=a$ is just the value $a$ with $e{}^a=x$. The construction mentioned above is shown in the figure below.
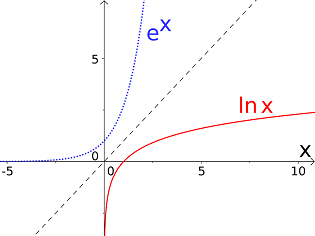
The following properties of the natural logarithmic function can be seen from the graph:

• The function $\ln$ is strictly increasing.
  
• Approaching zero from the right on the $x$-axis, $\ln (x)$ takes ever larger negative values: We note that the graph of $\ln$ gets arbitrarily close to the negative vertical axis ($y$-axis).
  
• At the point $x=1$ the natural logarithmic function takes the value $0$, i.e. $\ln (1)=0$.
  

As well as the natural logarithmic function there are other logarithmic functions, which each correspond to a certain exponent.

Normally, the logarithmic function cannot be calculated directly. Since it is defined as the inverse function of the exponential function, one generally tries to rewrite its input as a power and reads off the exponent.

Here, the base of the logarithmic function has to be observed, for example, we have

${\displaystyle {\log }_2(64)\mathrm{\hspace{0.5em}\hspace{0.5em}}=\mathrm{\hspace{0.5em}\hspace{0.5em}}{\log }_2(2^6)\mathrm{\hspace{0.5em}\hspace{0.5em}}=\mathrm{\hspace{0.5em}\hspace{0.5em}}6\hspace{0.5em},\hspace{0.5em}\mathrm{\hspace{0.5em}\hspace{0.5em}}\text{but}\mathrm{\hspace{0.5em}\hspace{0.5em}}\hspace{0.5em}{\log }_4(64)\mathrm{\hspace{0.5em}\hspace{0.5em}}=\mathrm{\hspace{0.5em}\hspace{0.5em}}{\log }_4(4^3)\mathrm{\hspace{0.5em}\hspace{0.5em}}=\mathrm{\hspace{0.5em}\hspace{0.5em}}3\hspace{0.5em}.}$



In mathematics and in the sciences the following logarithmic functions are frequently used and thus have their own dedicated names:

• Logarithmic function to the base $10$: denoted by ${\log }_{10}(x)=\text{lg}(x)$ or sometimes only by $\log (x)$. This logarithmic function is associated to the powers of ten and is used, for example, in chemistry for the calculation of the pH level.
  
• Logarithmic function to the base $2$: denoted by ${\log }_2(x)=\text{ld}(x)$. This logarithmic function is relevant in computer science.
  
• Logarithmic function to the base $e$: denoted by ${\log }_e(x)=\ln (e)$. The natural logarithmic function is mostly inadequate for practical calculations (unless the expression is a power of $e$). It is called natural since the exponential function with base $e$, from a mathematical point of view, is simpler than the general exponential function (e.g. because $e{}^x$ is its own derivative, but $b^x$ for $b\ne e$ is not).
  

There are several calculation rules for the logarithmic function, which will be explained in the next section.