Chapter 6 Elementary Functions

Section 6.2 Linear Functions and Polynomials

6.2.3 Linear Functions

Starting from the identity function, more complex functions - so-called linear functions - can be constructed. So, for example, one can think of a function that assigns to every real number twice its value or $\pi$ times its value, etc., e.g.

${\displaystyle f:\mathrm{\hspace{0.5em}\hspace{0.5em}}\{\begin{array}{ccc}\hfill ℝ& \hfill \to \hfill & ℝ\hfill \\ \hfill x& \hfill ⟼\hfill & 2x\hfill \end{array}}$
or

${\displaystyle g:\mathrm{\hspace{0.5em}\hspace{0.5em}}\{\begin{array}{ccc}\hfill ℝ& \hfill \to \hfill & ℝ\hfill \\ \hfill x& \hfill ⟼\hfill & \pi x\hspace{0.5em}.\hfill \end{array}}$

               
               
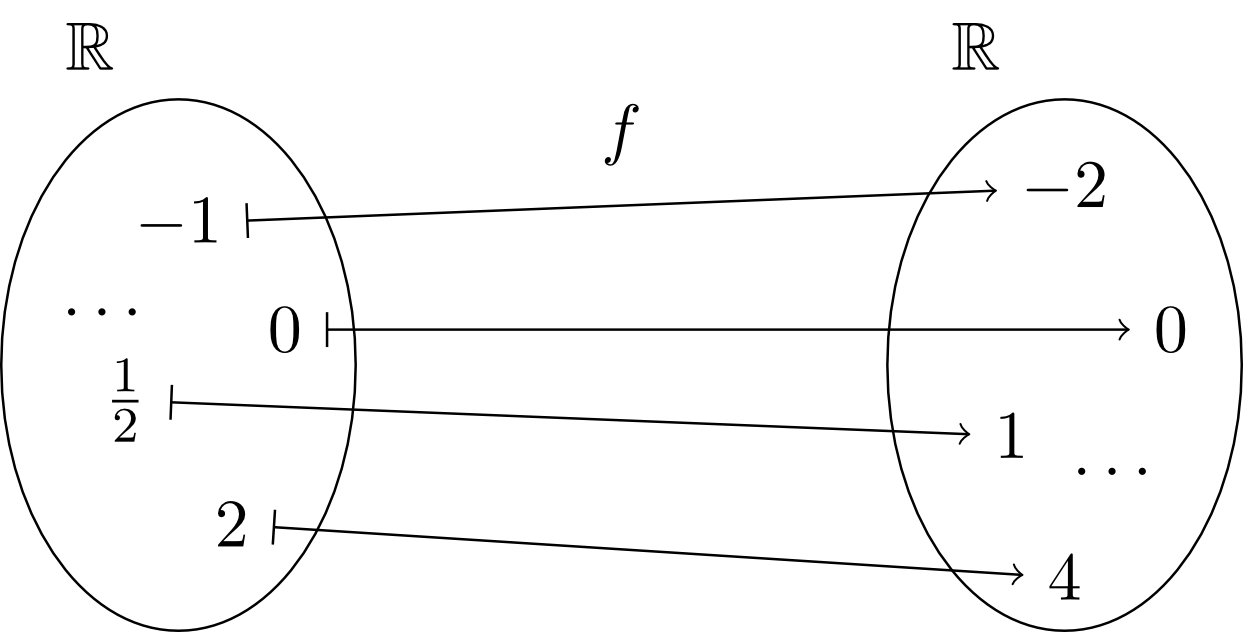
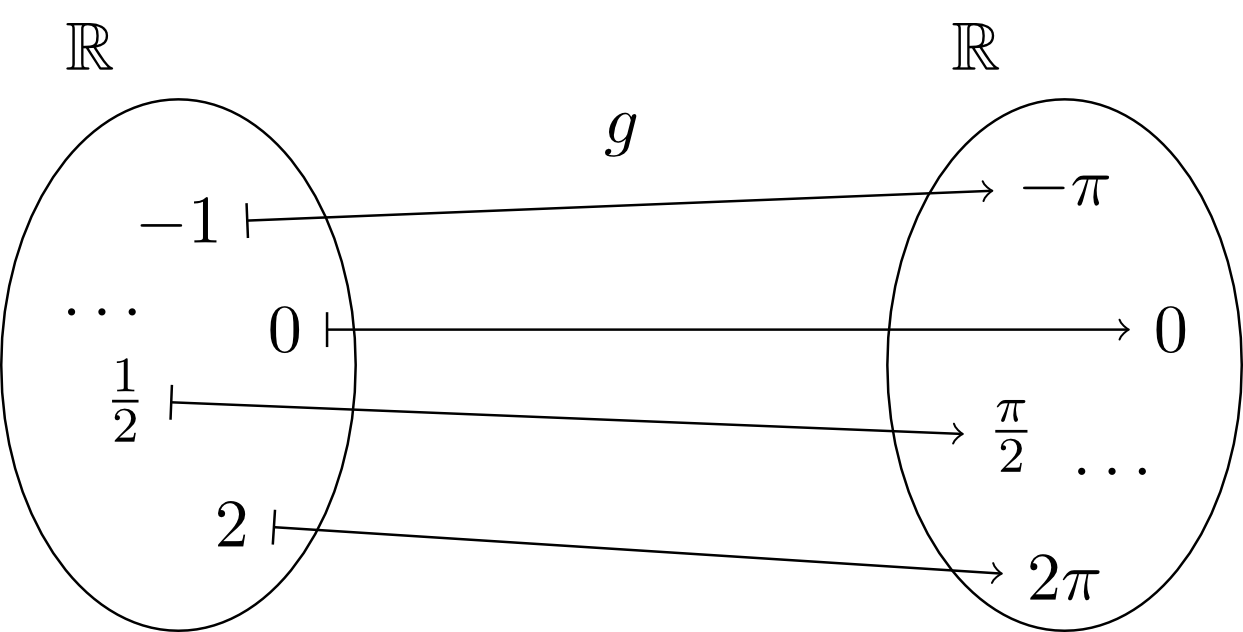
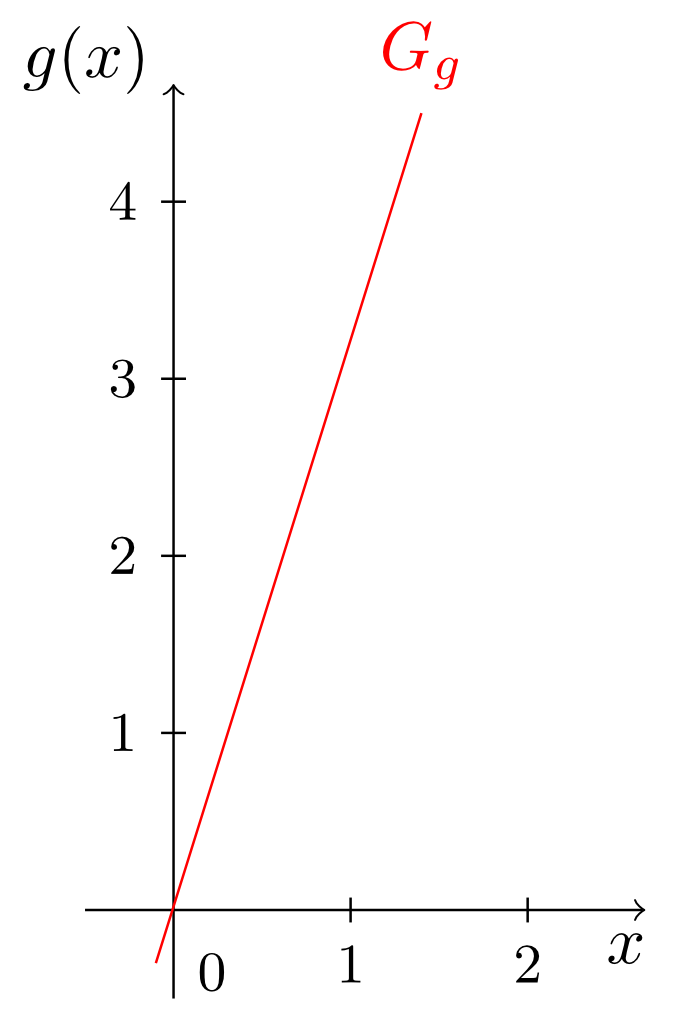
Hence, all linear functions (except for the zero function, see below) also have the entire set of real numbers as their ranges ($W_f,W_g=ℝ$). The factor that multiplies each real number in such a linear function is called slope of the linear function. Often, also for linear functions one does not like to specify a certain function with a specific slope, but an arbitrary function with an arbitrary slope $m\in ℝ$:

${\displaystyle f:\mathrm{\hspace{0.5em}\hspace{0.5em}}\{\begin{array}{ccc}\hfill ℝ& \hfill \to \hfill & ℝ\hfill \\ \hfill x& \hfill ⟼\hfill & mx\hspace{0.5em}.\hfill \end{array}}$


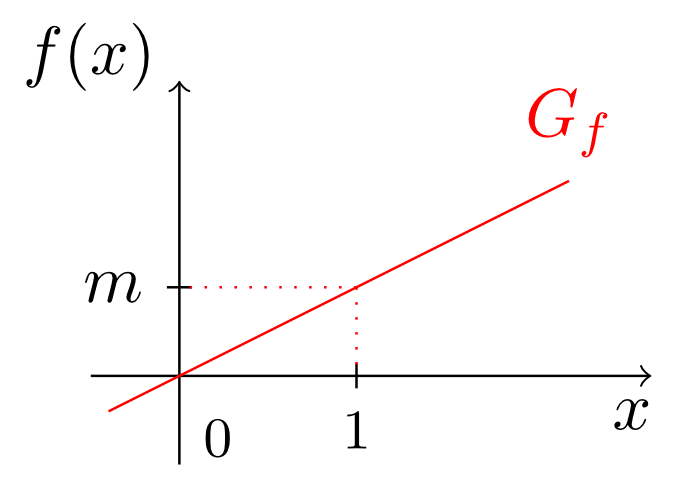
Where does the term slope of a linear function come from? If the difference in height by which the graph is rising vertically is divided by the corresponding length in the horizontal direction, then one obtains the slope $m$. So $m=\frac{f(x_2)-f(x_1)}{x_2-x_1}$ for $x_1<x_2$.