Chapter 6 Elementary Functions
Section 6.2 Linear Functions and Polynomials6.2.2 Constant Functions and the Identity
so-called constant functions assign to every number in the domain exactly the same constant number in the target set , e.g. the constant number , in the following way:
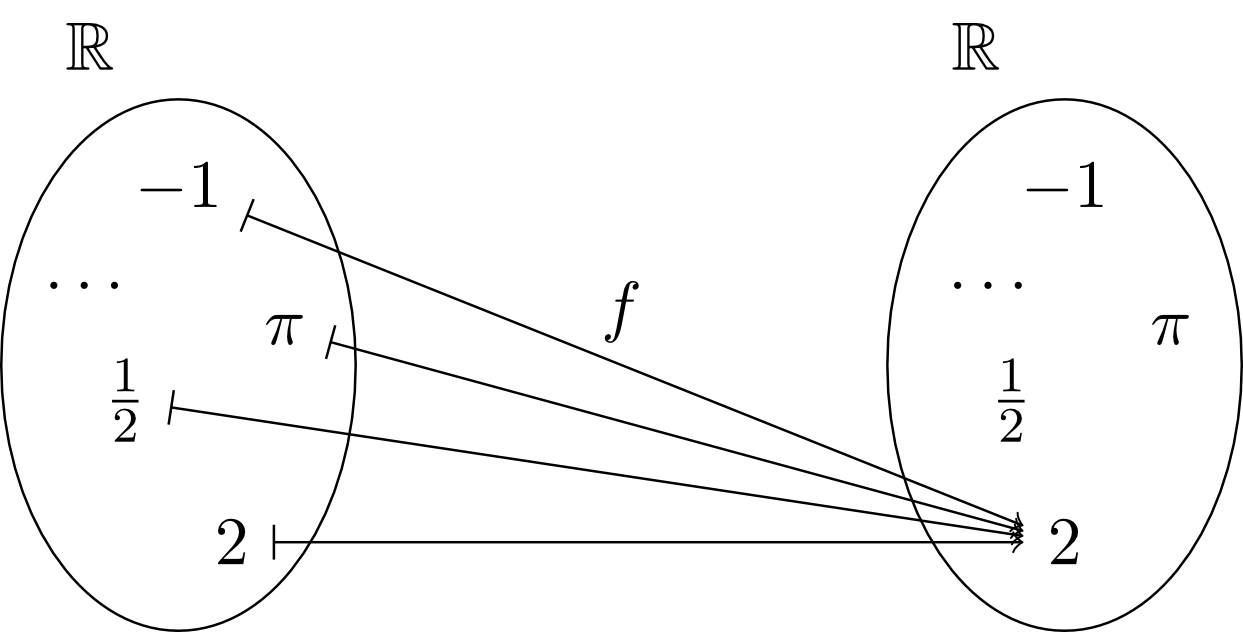
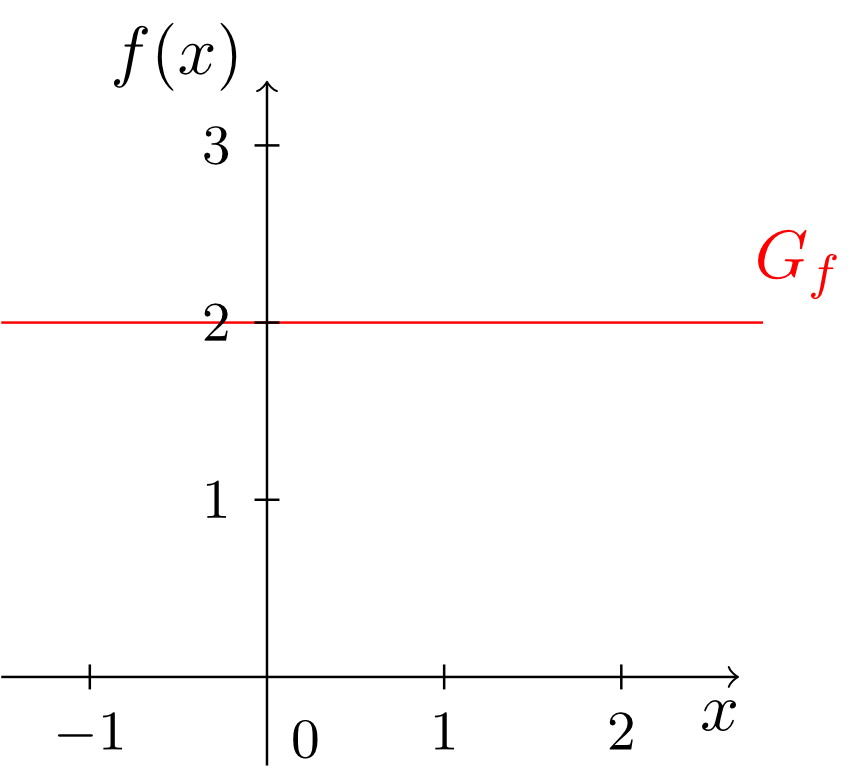
Here, we then have for all . Hence, the range of this function consists only of the set .
The identity function on is the function that assigns each real number to itself. This is written as follows:
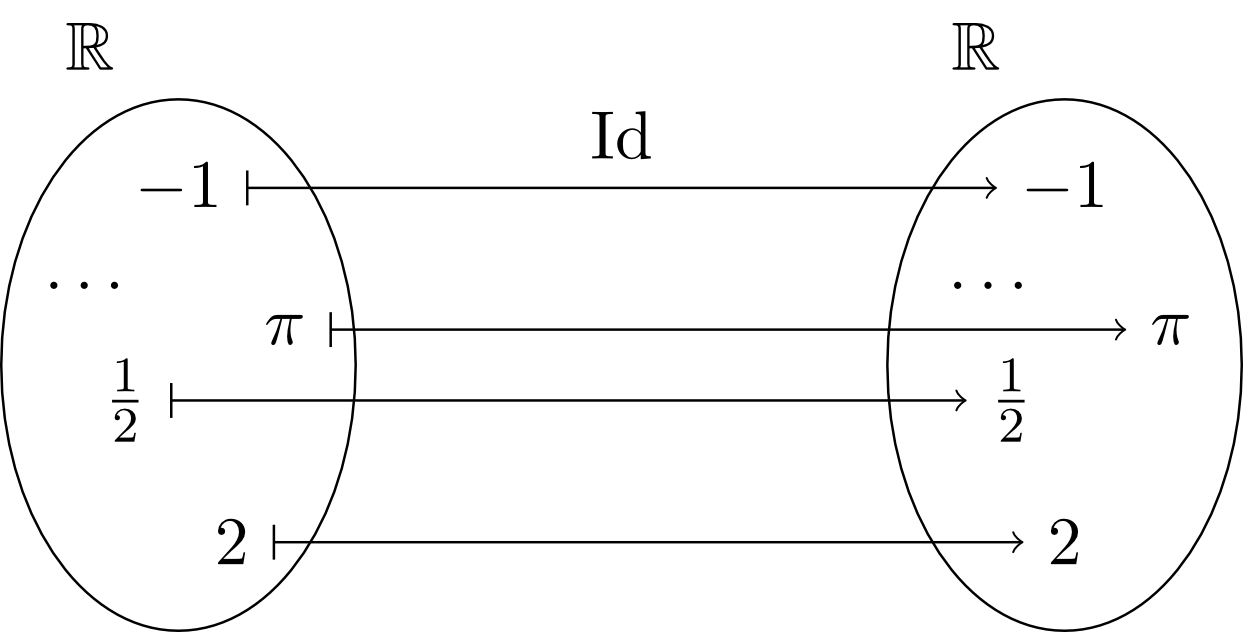
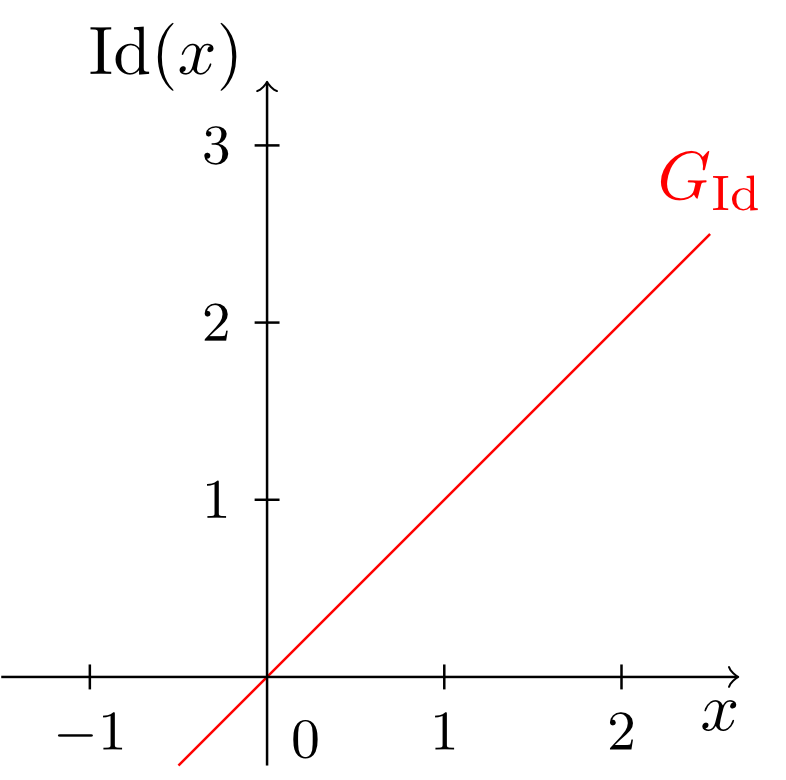
Here, we then have for all . Hence, the range of is the set of real numbers (). Furthermore, the identity function is (obviously) a strictly increasing function.
 Onlinebrückenkurs Mathematik
Onlinebrückenkurs Mathematik