Chapter 6 Elementary Functions

Section 6.2 Linear Functions and Polynomials

6.2.6 Monomials

In addition to the linear affine functions studied in the previous section, we can also think of functions that assign to every real number a non-negative integer power of the number. An example is the function

${\displaystyle g:\mathrm{\hspace{0.5em}\hspace{0.5em}}\{\begin{array}{ccc}\hfill ℝ& \hfill \to \hfill & ℝ\hfill \\ \hfill x& \hfill ⟼\hfill & x^2\hspace{0.5em}.\hfill \end{array}}$

       
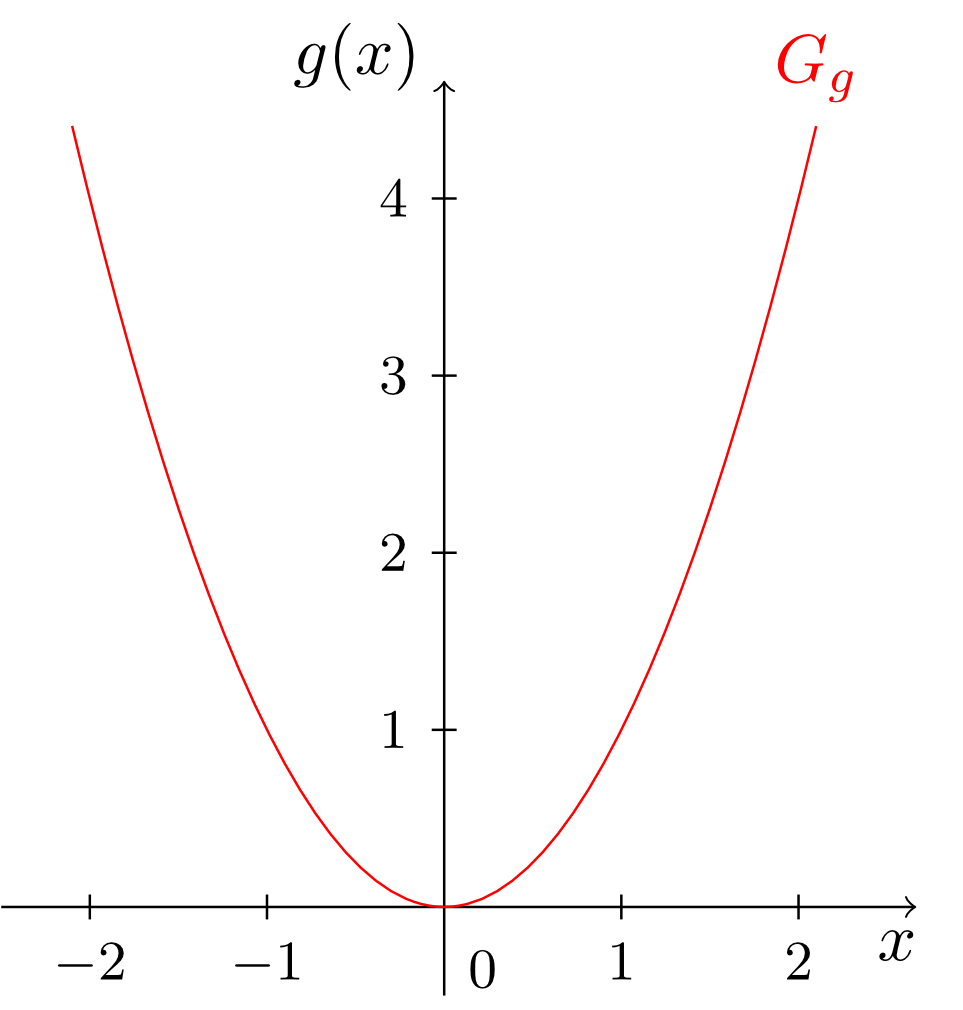
This works for every non-negative integer exponent, and generally this function is written as

${\displaystyle f:\mathrm{\hspace{0.5em}\hspace{0.5em}}\{\begin{array}{ccc}\hfill ℝ& \hfill \to \hfill & ℝ\hfill \\ \hfill x& \hfill ⟼\hfill & x^n\hfill \end{array}}$
with $n\in \mathbb{N}{}_0$, and it is called a monomial. The exponent $n$ of a monomial is called the degree of the monomial. For example, the function $g$ described at the beginning of this section is a monomial of degree $2$.
The monomial of degree $2$ is called the standard parabola. The monomial of degree $3$ is called the cubic standard parabola. The figure below shows the graphs of a few monomials.

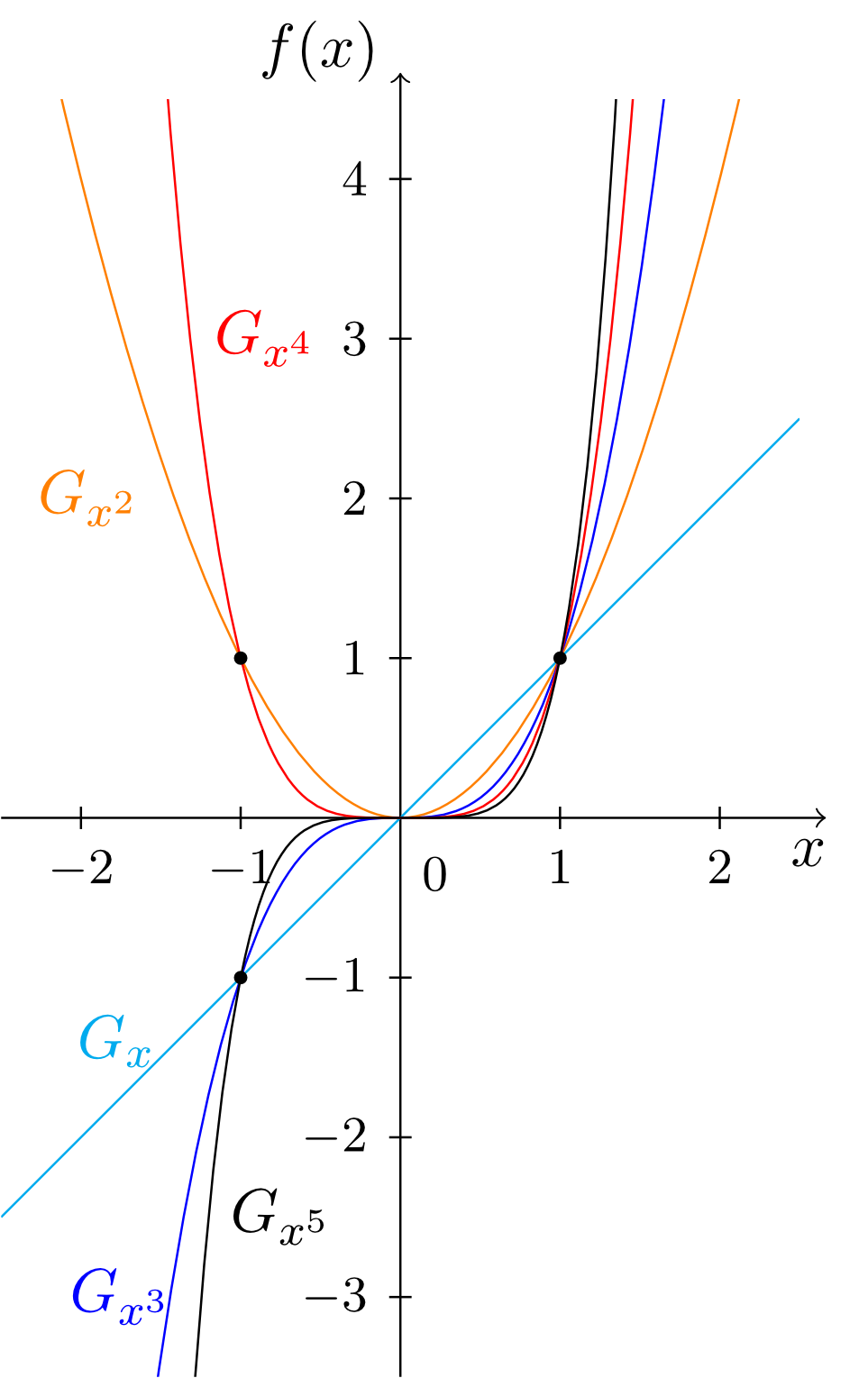
On the basis of these graphs, we now summarise some conclusions on monomials: There is a fundamental difference between monomials (with the mapping rule $f(x)=x^n$, $n\in \mathbb{N}$) of even and odd degree. The range of monomials of an even non-zero degree is always the set $[0;\infty )$, while monomials of odd degree have the range $ℝ$. Furthermore, we always have

${\displaystyle f(1)=1^n=1\hspace{0.5em},}$


${\displaystyle f(0)=0^n=0}$
and

${\displaystyle f(-1)=\{\begin{array}{cc}\hfill 1& \text{for}\hspace{0.5em}n\hspace{0.5em}\text{even}\hfill \\ \hfill -1& \text{for}\hspace{0.5em}n\hspace{0.5em}\text{odd .}\hfill \end{array}}$
Moreover, we have

${\displaystyle \{\begin{array}{cc}\hfill x>x^2>x^3>x^4>\dots & \text{for}\hspace{0.5em}x\in (0;1)\hfill \\ \hfill x<x^2<x^3<x^4<\dots & \text{for}\hspace{0.5em}x\in (1;\infty )\hspace{0.5em}.\hfill \end{array}}$