Chapter 6 Elementary Functions
Section 6.2 Linear Functions and Polynomials6.2.10 Asymptotes
In this section we will study how rational functions behave as tends to infinity if the degree of the polynomial in the numerator is less than or equal to the degree of the polynomial in the denominator. An example of this is the function
In the function , the degree of the polynomial in the numerator is , and degree of the polynomial in the denominator is . Other examples were investigated in the previous Section 6.2.9.
Example 6.2.21
Let us consider the function
Its mapping rule is a sum of a polynomial (of degree ) and a rational term. By finding the common denominator it is easy to transform into a rational form in which the degree of the polynomial in the numerator equals the degree of the polynomial in the denominator:
Thus, we can rewrite in the form
and we now consider the corresponding graph.
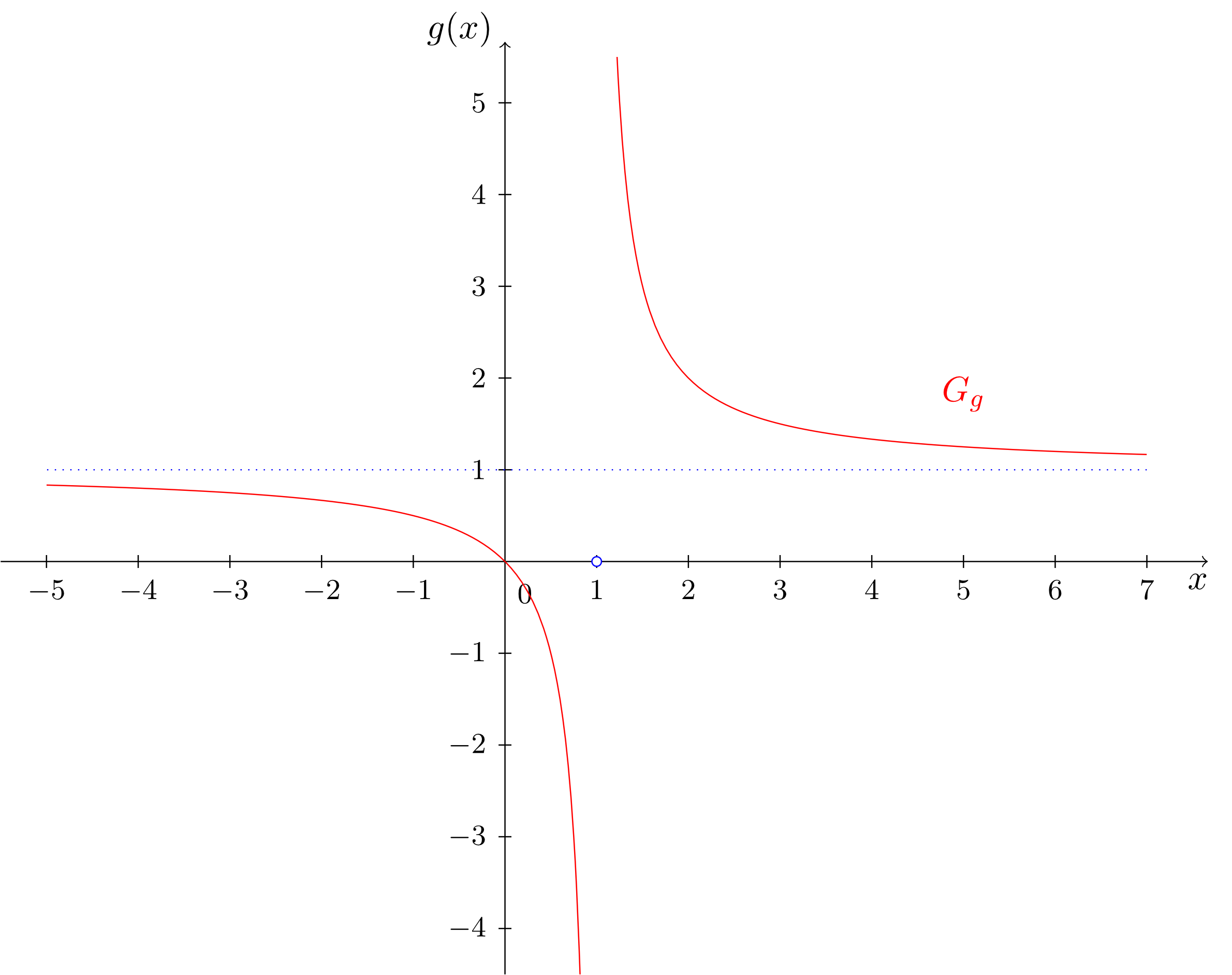
Besides the pole and the singularity at , we see that the value is of specific relevance. Obviously, this value is never taken by the function . Thus, the range of is . Instead, for "very large" values ( tends to plus infinity) and "very small" values ( tends to minus infinity) of the independent variable , the function approaches its limiting value indefinitely without ever reaching it for any real number .
This can be seen from the mapping rule as follows. For "very large" (, , , etc.) or "very small" (, , , etc.) values of , the rational part approaches since occurs in the denominator. In general, for these values of , only the polynomial part of the mapping rule remains. This part can be described by a - in this case constant - function that is called an asymptote of the function :
Since this is a constant function, it is also called a horizontal asymptote.
Its mapping rule is a sum of a polynomial (of degree ) and a rational term. By finding the common denominator it is easy to transform into a rational form in which the degree of the polynomial in the numerator equals the degree of the polynomial in the denominator:
Thus, we can rewrite in the form
and we now consider the corresponding graph.

Besides the pole and the singularity at , we see that the value is of specific relevance. Obviously, this value is never taken by the function . Thus, the range of is . Instead, for "very large" values ( tends to plus infinity) and "very small" values ( tends to minus infinity) of the independent variable , the function approaches its limiting value indefinitely without ever reaching it for any real number .
This can be seen from the mapping rule as follows. For "very large" (, , , etc.) or "very small" (, , , etc.) values of , the rational part approaches since occurs in the denominator. In general, for these values of , only the polynomial part of the mapping rule remains. This part can be described by a - in this case constant - function that is called an asymptote of the function :
Since this is a constant function, it is also called a horizontal asymptote.
Exercise 6.2.22
Identify the asymptotes of the function
and the asymptote of the hyperbola described in Section 6.2.8.
and the asymptote of the hyperbola described in Section 6.2.8.
Info 6.2.23
A rational function with the polynomial of degree in the numerator and the polynomial of degree in the denominator of the form
has a constant function (or a horizontal line) as an asymptote if . In particular, the zero function is the asymptote in the case .
 Onlinebrückenkurs Mathematik
Onlinebrückenkurs Mathematik