6.4.1 Introduction

A bacterial culture starts with $500$ bacteria and doubles in size every $13$ minutes. We would like to know how many bacteria will be in the culture after $1$ hour and $15$ minutes (i.e. after $75$ minutes).
As a first try we can create a simple table of values that lists the number of bacteria in the population at the beginning ($t=0$ min), after $t=13$ min, after $t=26$ min, etc., i.e. at multiples of the $13$ minutes duplication time: From the table we can estimate that the answer to our question will be between $16\hspace{0.5em}000$ and $32\hspace{0.5em}000$, probably closer to $32\hspace{0.5em}000$. What about a (more) precise answer? For this, we need to know the functional relation between the values of $t$ and the number of bacteria. In the figure below the graph of a function $p$ is shown; so to speak, this graph closes the gaps between the isolated points that correspond to the pairs of values in the table and are plotted as well. The corresponding mapping rule assigns to every real valued point in time a number of bacteria. As we will see, the corresponding function is an exponential function.

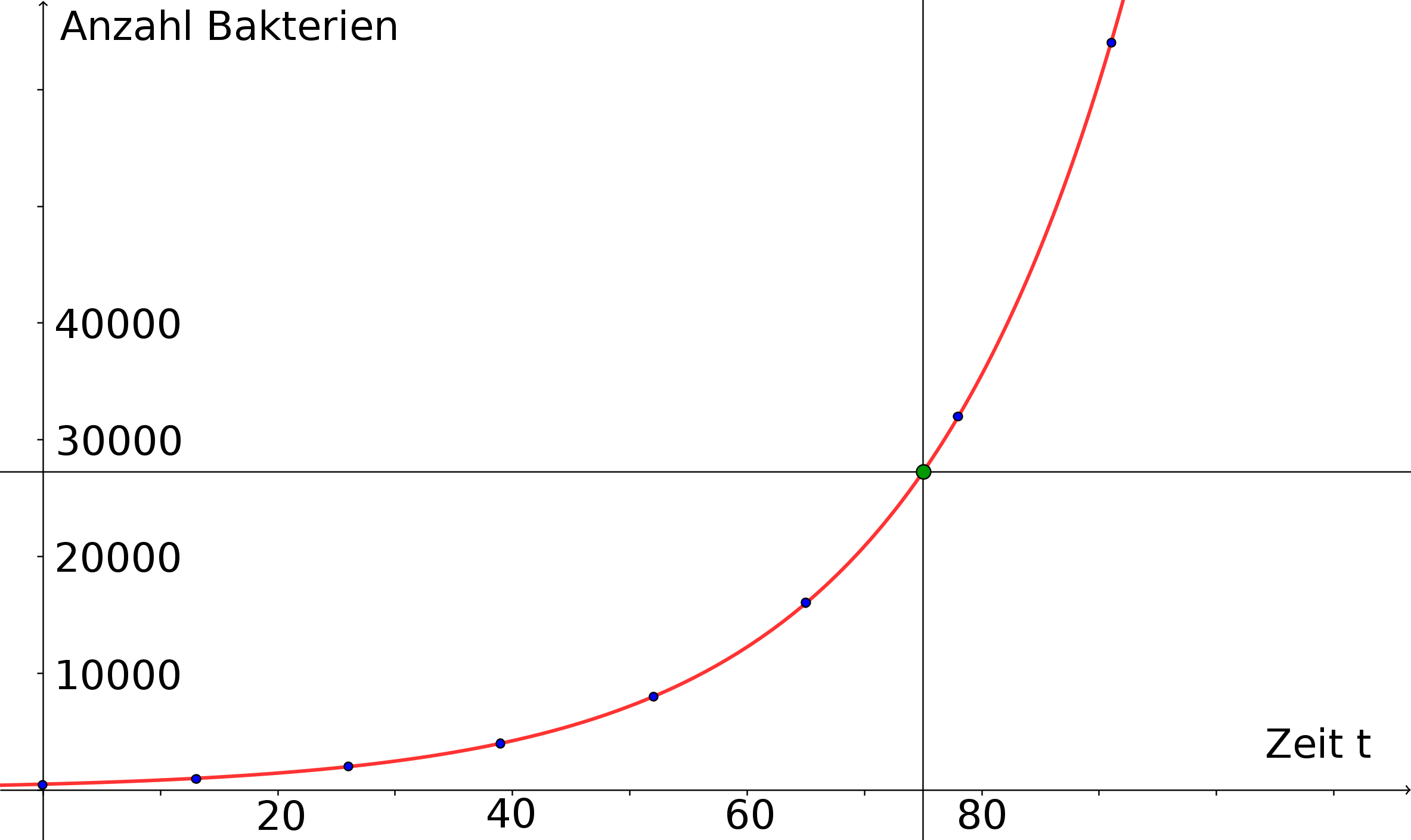
From the graphical representation, the required number of bacteria can be read off a bit more precisely. However, for the exact specification we need the mapping rule underlying the graph, which we will first simply state here:

${\displaystyle p:[0;\infty )\to (0;\infty )\mathrm{\hspace{0.5em}\hspace{0.5em}}\text{with}\mathrm{\hspace{0.5em}\hspace{0.5em}}t⟼p(t)=500·2^{(t/13)}\hspace{0.5em}.}$

(In Exercise 6.4.3 we will give a reason for this functional relation.)
For $t=75$ (measured in minutes) we obtain the function value

${\displaystyle p(75)=500·2^{(75/13)}\approx 500·54.539545\approx 27\hspace{0.5em}270\hspace{0.5em}.}$

Hence, after $75$ minutes approx. $27\hspace{0.5em}270$ bacteria live in the considered population.