Chapter 6 Elementary Functions

Section 6.3 Power Functions

6.3.2 Radical Functions

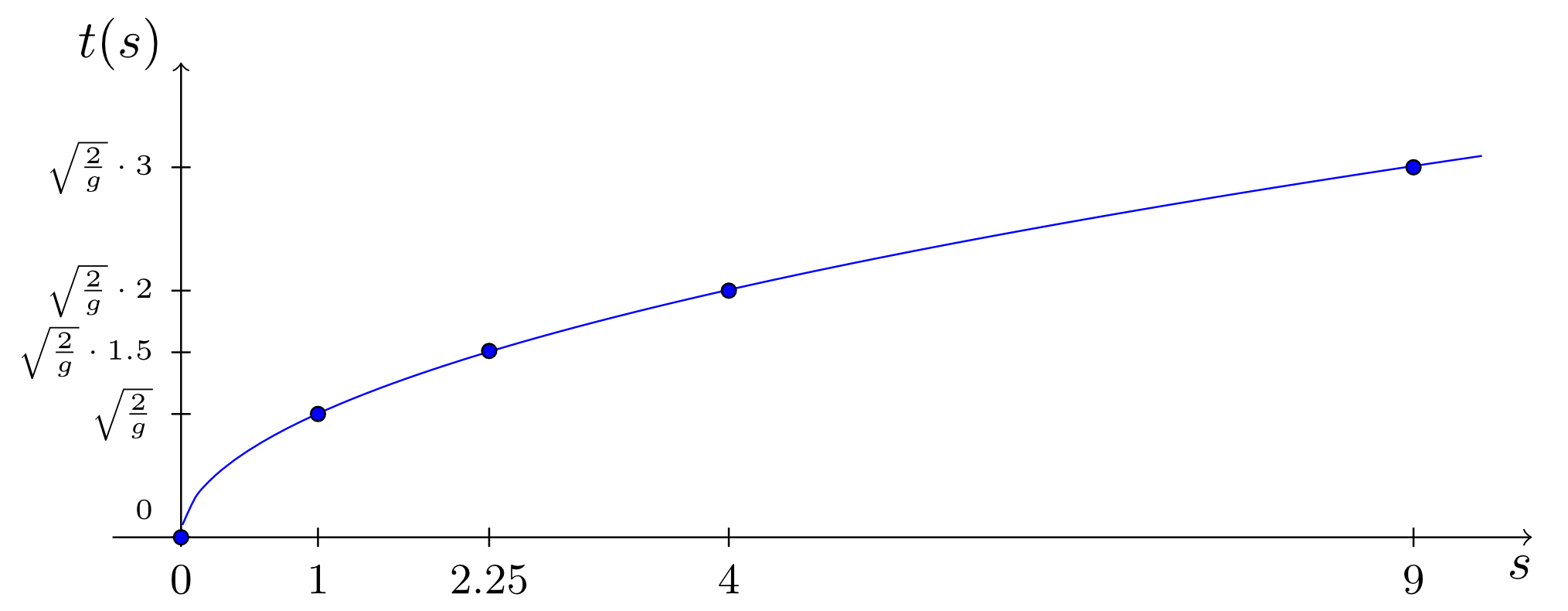
This example shows that functions with mapping rules that contain roots of the independent variables occur naturally in applications of mathematics.
For natural numbers $n\in \mathbb{N}$, $n>1$, the functions

${\displaystyle f_n:\mathrm{\hspace{0.5em}\hspace{0.5em}}\{\begin{array}{ccc}\hfill D_{f_n}& \hfill \to \hfill & ℝ\hfill \\ \hfill x& \hfill ⟼\hfill & \sqrt[n]{x}=x^{\frac{1}{n}}\hfill \end{array}}$
are called radical functions. Obviously, these include the square root $f_2(x)=\sqrt{x}$, the cube root $f_3(x)=\sqrt[3]{x}$, the fourth root $f_4(x)=\sqrt[4]{x}$, etc., as mapping rules of functions (see exponent rules).


Of great relevance is now the maximum domain $D_{f_n}$ that a radical function can have. Obviously, it depends on the exponent $n$ of the root which values of $x$ are allowed to be inserted in the mapping rule to obtain real values as a result. So we see that the square root $\sqrt{\hspace{0.5em}}$ has a real value as a result only for a non-negative number. However, if we consider the cube root $\sqrt[3]{\hspace{0.5em}}$, then we see that the cube root has a real value as a result for all real numbers, for example, $\sqrt[3]{-27}=-3$. Generally, we have:

Thus, the graphs of the first four radical functions, $f_2$, $f_3$, $f_4$, $f_5$, look like as in the figure below.

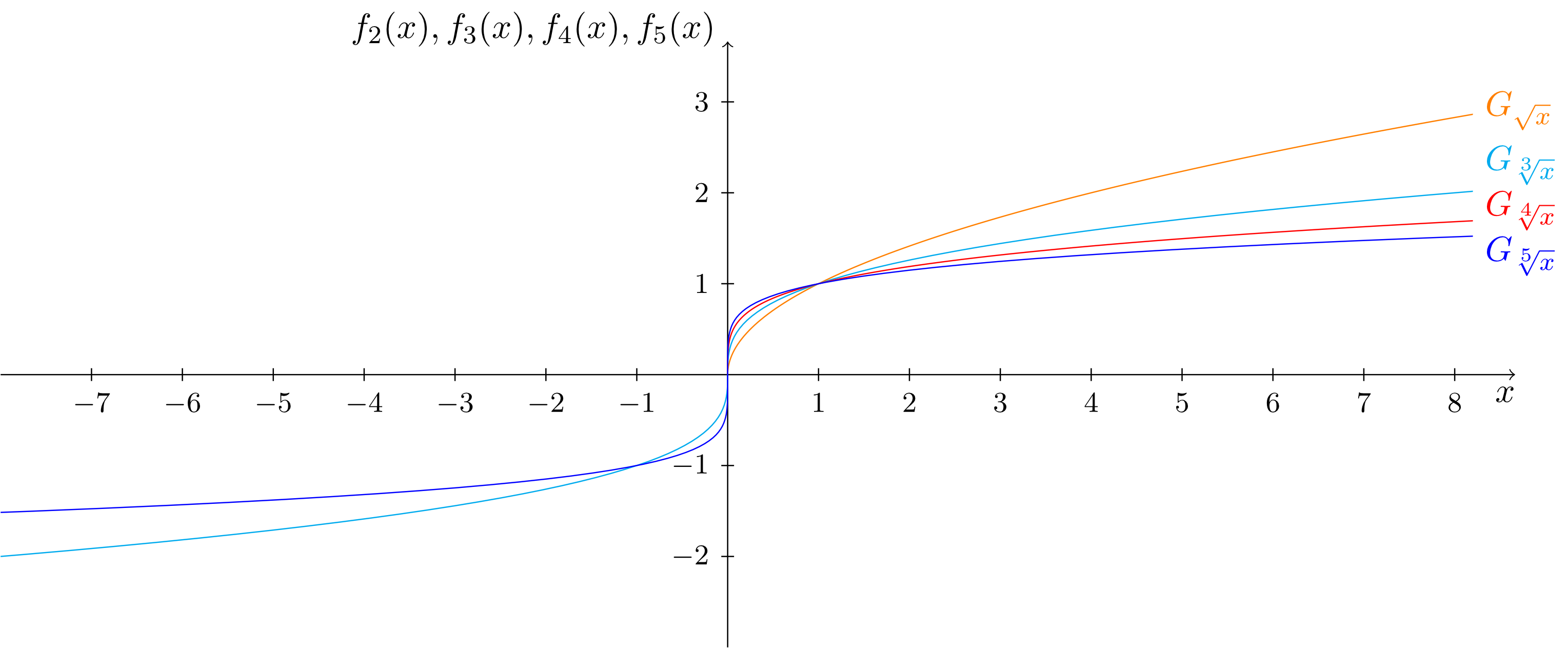
From the graphs, it can be seen that all radical functions are strictly increasing.