Chapter 6 Elementary Functions

Section 6.6 Properties and Construction of Elementary Functions

6.6.2 Symmetry


Info 6.6.1
 
A function f:ℝ→ℝ is called even or axially symmetric if, for all x∈ℝ, we have

f(x)=f(-x) .

Analogously, a function is called odd or centrally symmetric if, for all x∈ℝ, we have

f(x)=-f(-x) .


These two symmetry conditions for functions allow us to make conclusions about the behaviour of the graphs. For even functions, a reflection across the vertical axis does not change the graph, and for odd functions, a reflection across the origin does not change the graph. A few illustrative examples are listed below.
Example 6.6.2
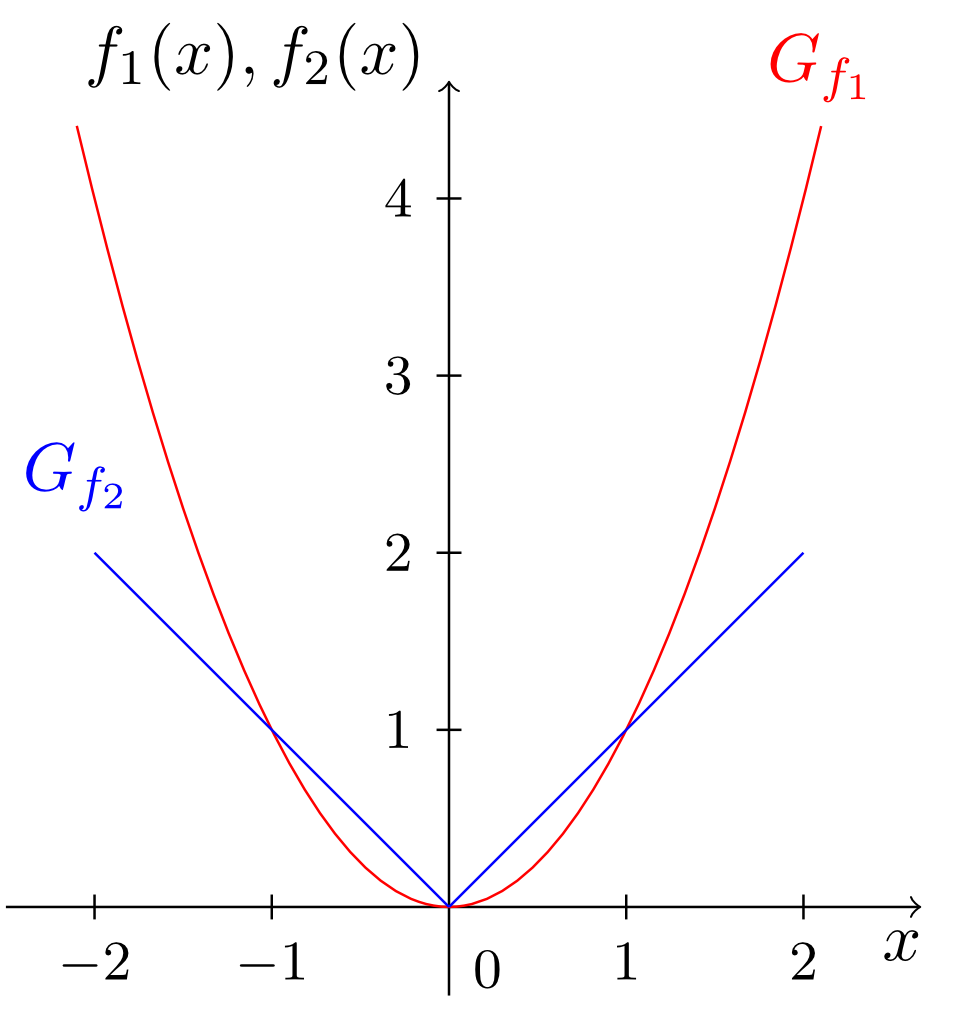
  • The functions

    f1 :  { ℝ→ℝ x⟼ x2

    and

    f2 :  { ℝ→ℝ x⟼|x| ,

    i.e. the standard parabola (see Section 6.2.6) and the absolute value function (see Section 6.2.5), are examples of even functions. We have f1 (-x)=(-x )2 = x2 = f1 (x) and f2 (-x)=|-x|=|x|= f2 (x) for all x∈ℝ. The graphs of these two functions are symmetric under reflection across the vertical axis.

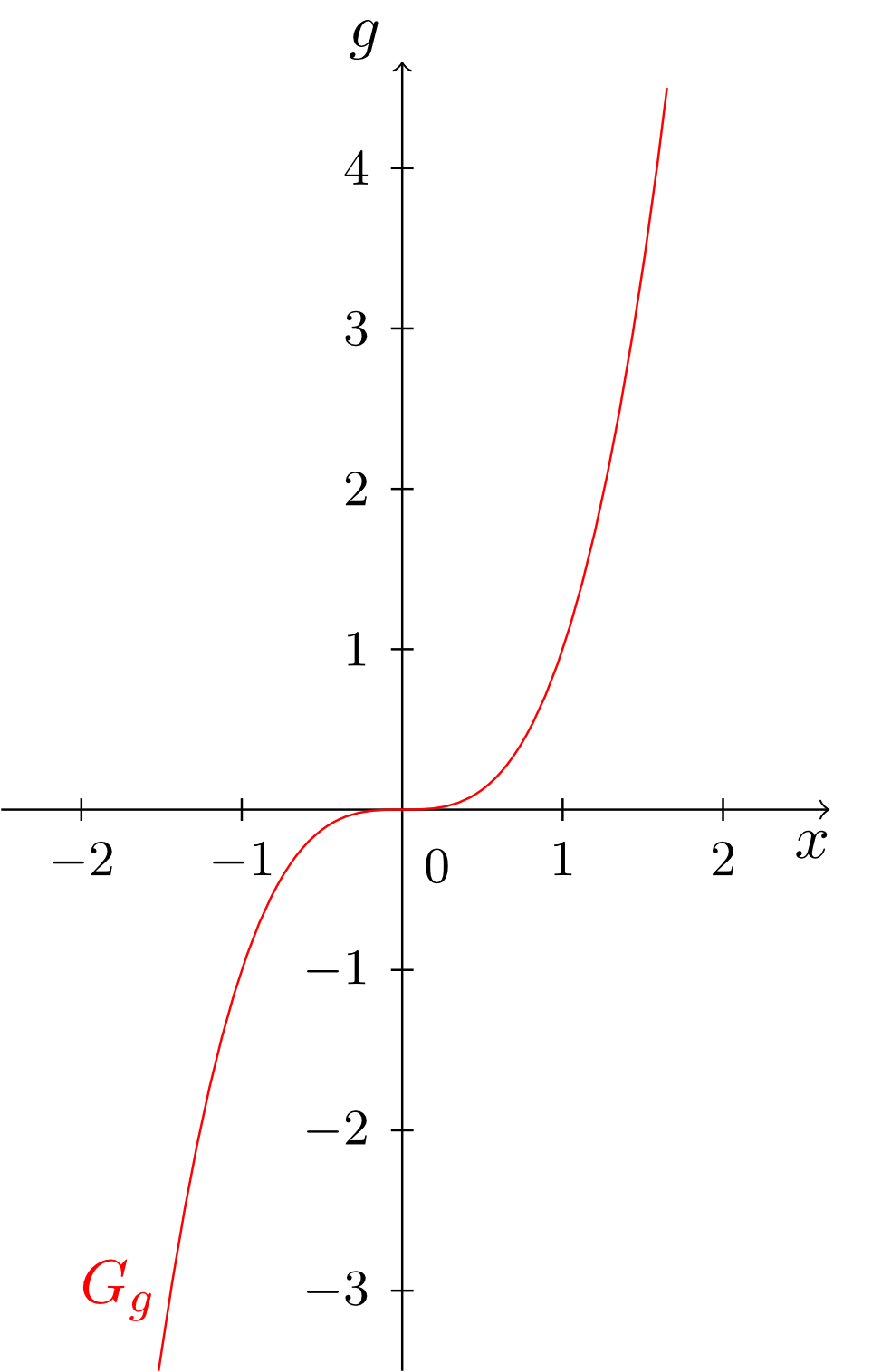
  • The function

    g:  { ℝ→ℝ x⟼ x3  ,

    i.e. the cubic parabola (see Section 6.2.6), is an example of an odd function. We have g(-x)=(-x )3 =- x3 =-g(x) for all x∈ℝ. The graph of the function is centrally symmetric with respect to the origin.


Of course, the symmetry properties of functions can also be used if the domain of the function is not the entire set of real numbers. However, then the domain must contain the number 0 in the middle of the interval. An example of this case is the tangent function in the exercise below.
Exercise 6.6.3
Specify whether the following functions are even, odd or non-symmetric.


  • f:  { ℝ→ℝ x⟼ex




  • g:  { ℝ→ℝ y⟼sin(y)




  • h:  { (- π 2 ; π 2 )→ℝ α⟼tan(α)




  • i:  { ℝ→ℝ u⟼cos(u)




  • j:  { ℝ→ℝ x⟼42




: