Chapter 6 Elementary Functions

Section 6.6 Properties and Construction of Elementary Functions

6.6.3 Sums, Products, Compositions


In this section, we will now use the large collection of elementary functions that we acquired in this module to create new more complex functions out of this elementary functions. At different places throughout this module we already studied functions those mapping rules were composed of sums and products of simpler mapping rules. Of course, one can also take differences and, under certain conditions, quotients from mapping rule. The example below lists a few such combined functions.
Example 6.6.4
  • The function

    f:  { ℝ→ℝ x⟼x+sin(x)

    is the sum of the identity function (see Section 6.2.3) and the sine function (see Section 6.5). The graph of this function is shown in the figure below.

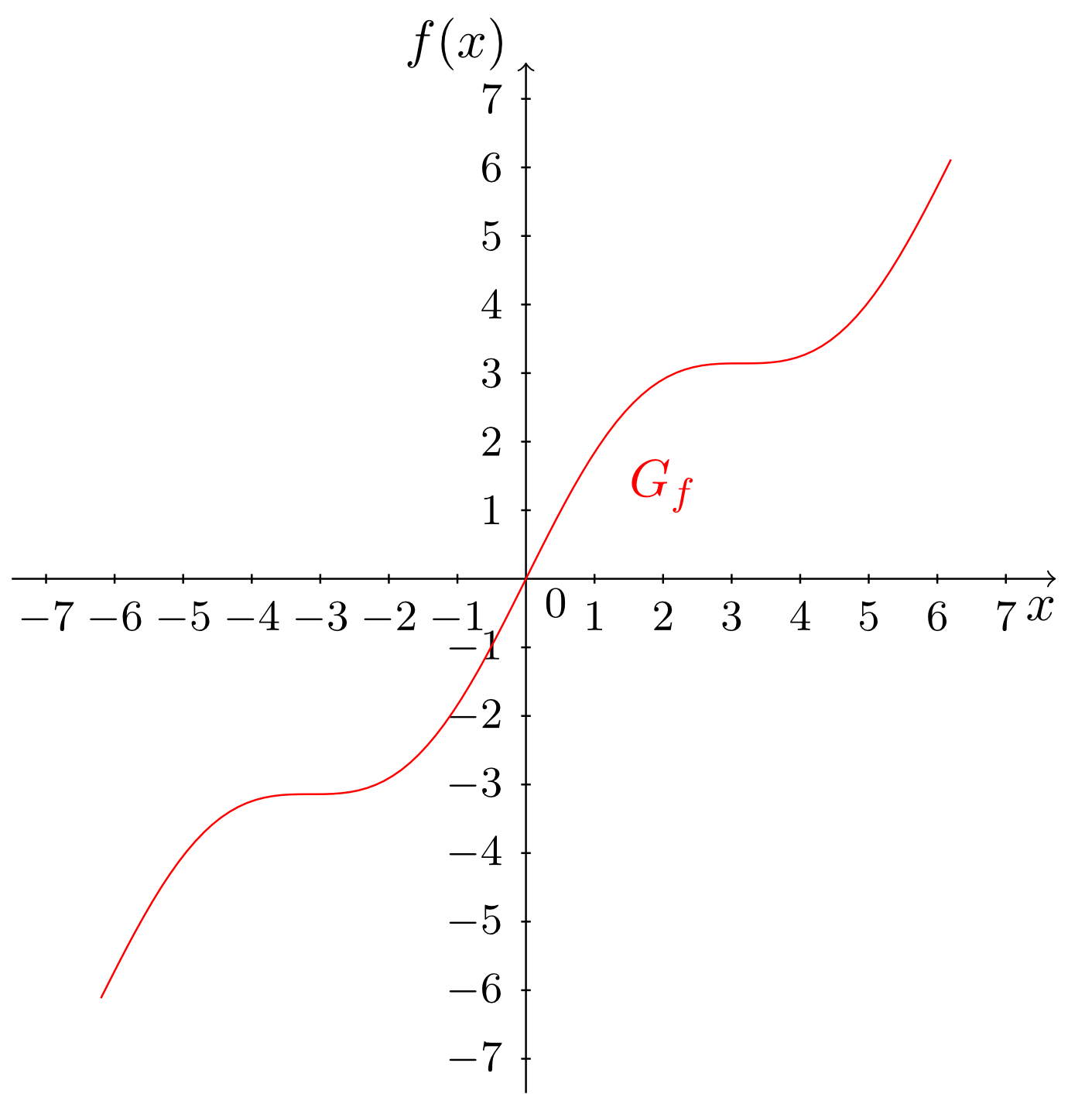
  • The function

    g:  { [1;2]→ℝ y⟼ y2 -ln(y)

    is the difference of the standard parabola (see Section 6.2.6) and the natural logarithmic function (see Section 6.4.4). The graph of this function is shown in the figure below.

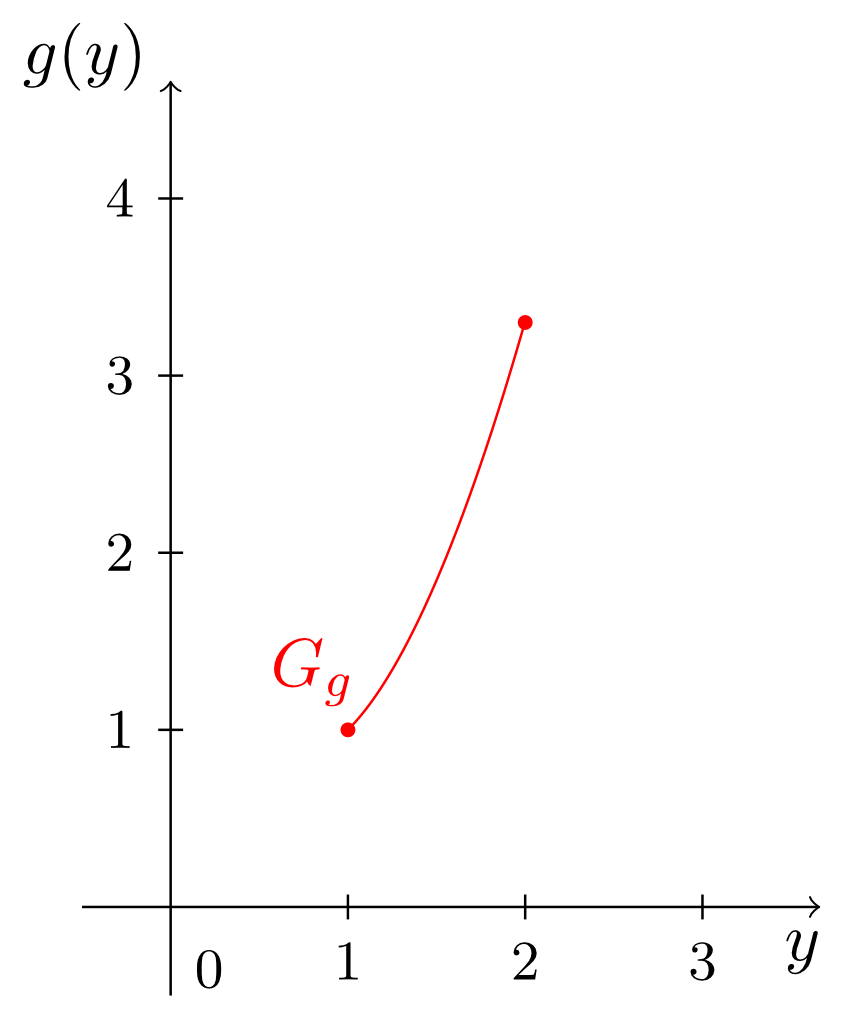
  • The function

    h:  { (0;∞)→ℝ x⟼ex 1 x

    is the product of the natural exponential function with the mapping rule ex (see Section 6.4.3) and the hyperbola with the mapping rule 1 x (see Section 6.2.8). The graph of this function is shown in the figure below.

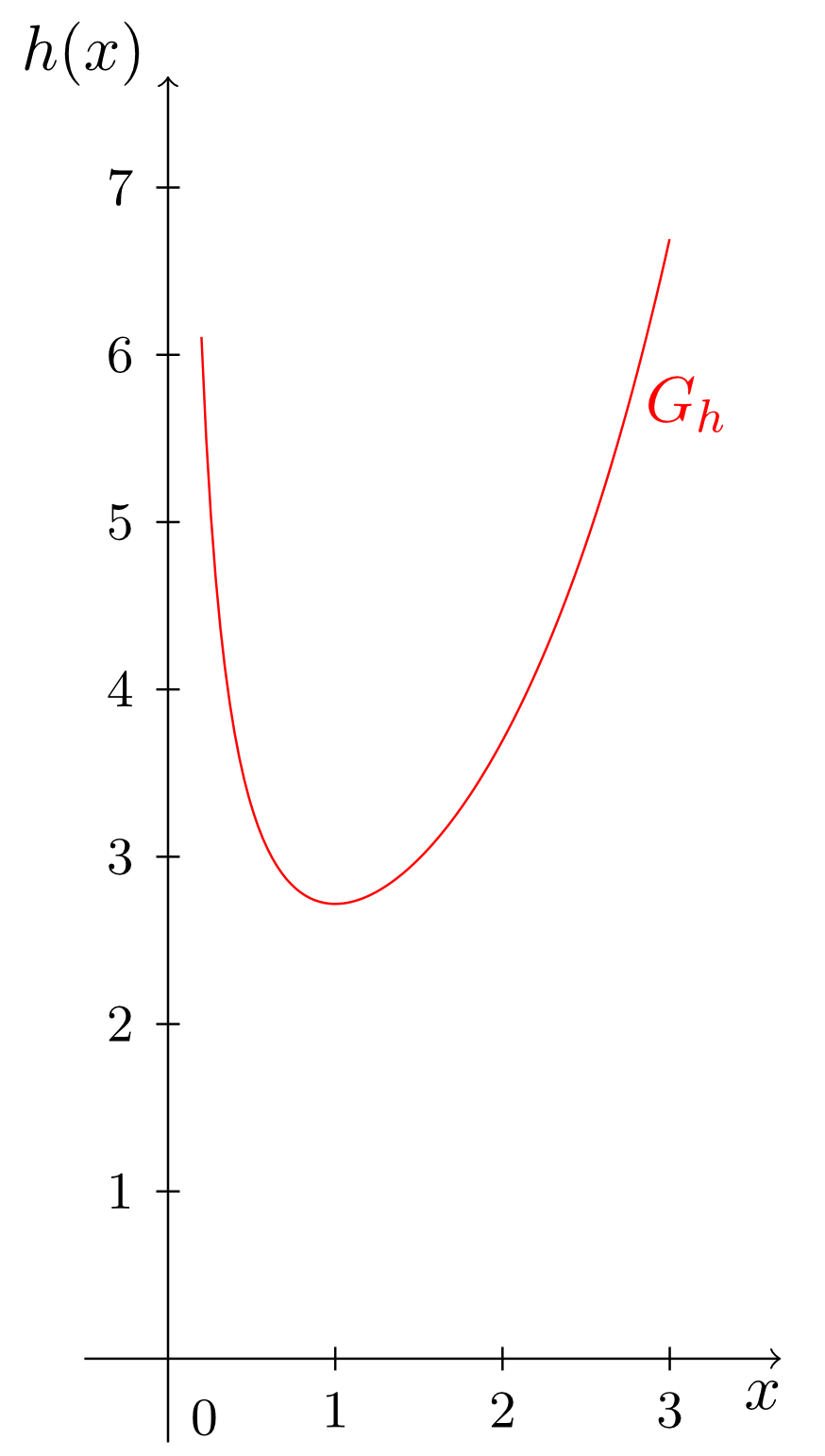
  • The function

    φ:  { ℝ→ℝ z⟼ cos(z) z2 +1

    is the quotient of the cosine function (see Section 6.5.3) and the polynomial of degree 2 (see Section 6.2.7) with the mapping rule z2 +1. The graph of this function is shown in the figure below.



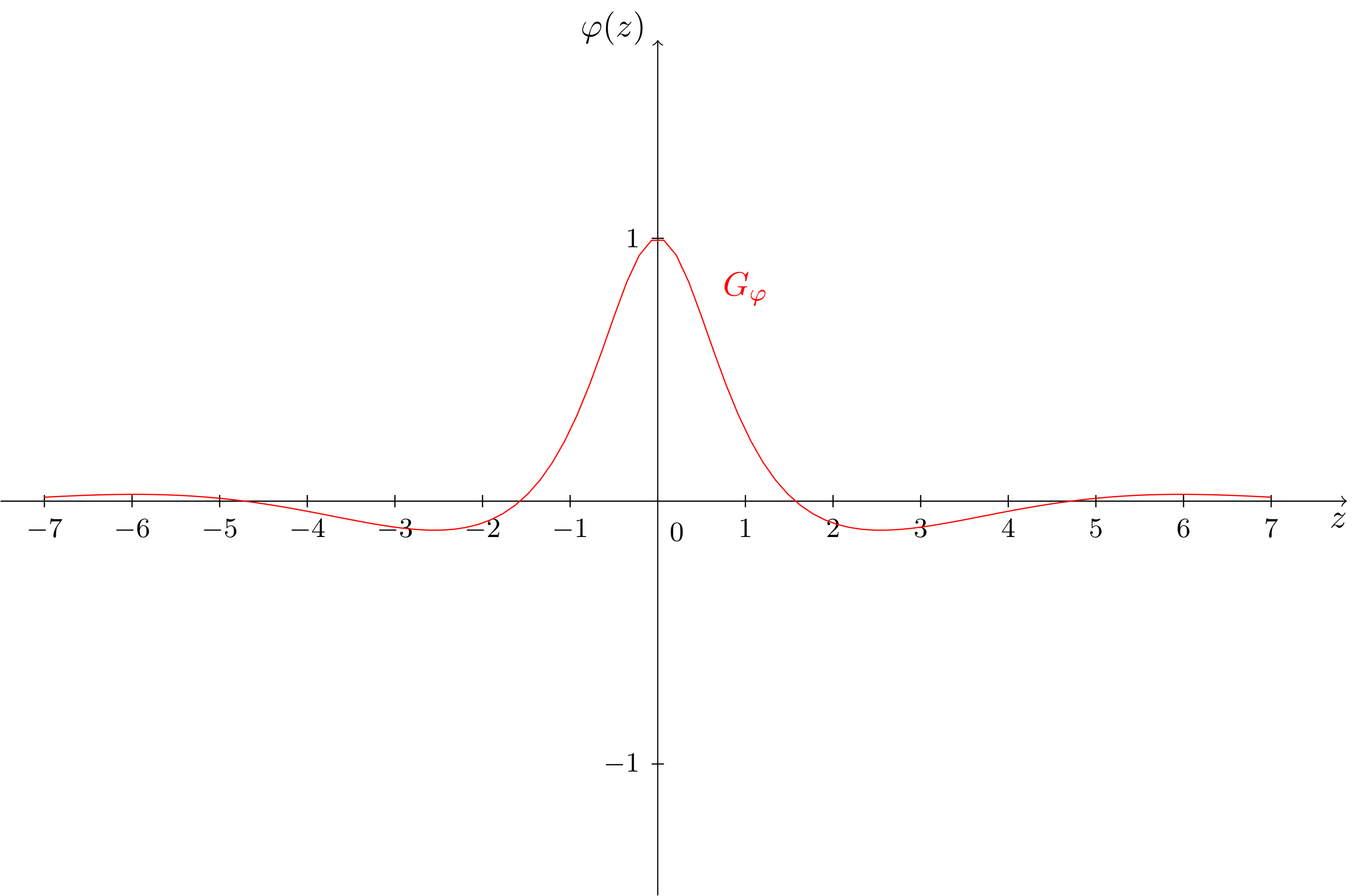
Exercise 6.6.5
Find further examples for elementary functions we studied in this module that were constructed from simpler elementary functions by combining sums, differences, product, or quotients.


Finally, there is another way to combine elementary functions to obtain new functions. This is the so-called composition of functions.
Let us consider a few examples.
Example 6.6.6
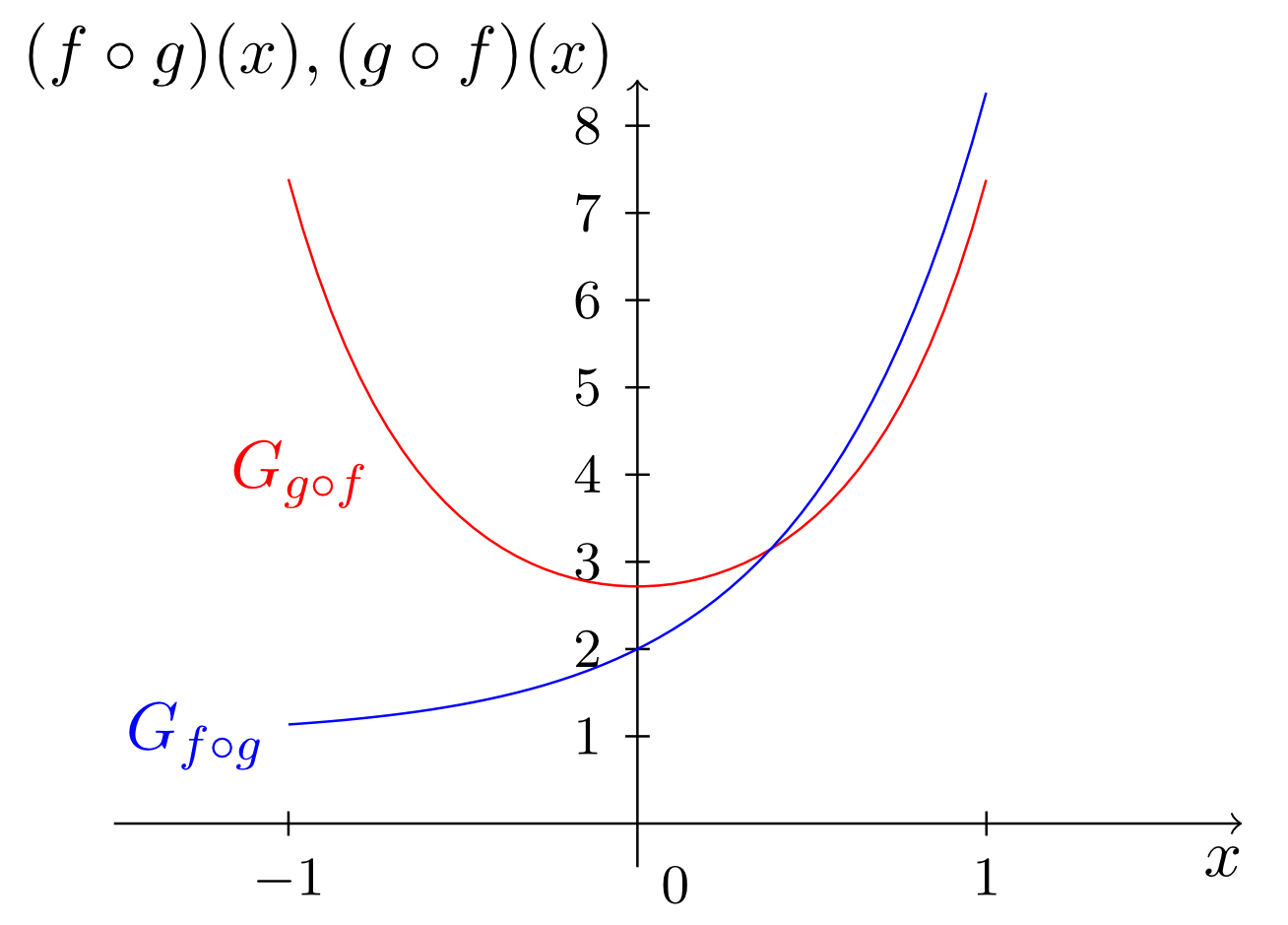
  • The functions

    f:  { ℝ→ℝ x⟼f(x)= x2 +1

    and

    g:  { ℝ→ℝ x⟼g(x)=ex

    can be composed in two ways. We can compose the function f∘g:ℝ→ℝ or the function g∘f:ℝ→ℝ. We obtain

    (f∘g)(x)=f(g(x))=f(ex )=(ex )2 +1=e2x +1 ,

    i.e.

    f∘g:  { ℝ→ℝ x⟼e2x +1 ,

    and

    (g∘f)(x)=g(f(x))=g( x2 +1)=e x2 +1  ,

    i.e.

    g∘f:  { ℝ→ℝ x⟼e x2 +1  .

    If we look at the graphs, we see that these are two completely different functions, i.e. the order of the composition is relevant.

  • If two functions such as

    h:  { ℝ→ℝ x⟼sin(x)

    and

    w:  { [0;∞)→ℝ x⟼x

    are composed, however, the domains of the functions have to be observed. For example, if we want to consider the composed function w∘h, then we have

    (w∘h)(x)=w(h(x))=w(sin(x))=sin(x) .

    Since the values of the sine function can also be negative but the square root only accepts non-negative values, the domain of the sine function has to be restricted accordingly such that the corresponding function values of the sine function are always non-negative, for example, by the restriction x∈[0;π]= Dw∘h . Thus, we have

    w∘h:  { [0;π]→ℝ x⟼sin(x) .



Exercise 6.6.7
Let the functions

f:  { ℝ→ℝ x⟼2x-3 



g:  { ℝ∖{0}→ℝ x⟼ 1 x


and

h:  { ℝ→ℝ x⟼sin(x)

be given. Specify the compositions f∘g, g∘f, h∘f, h∘g, f∘f, and g∘g. Restrict the domains, if necessary, such that the composition is allowed. However, for the composed function always use the maximum domain.



: