Chapter 6 Elementary Functions

Section 6.5 Trigonometric Functions

6.5.2 Sine Function

In Module 5 the trigonometric functions were introduced in Section 5.6 on right triangles, for example by the relation

${\displaystyle \begin{array}{ccccc}\hfill \sin (\alpha )& \hfill =\hfill & \hfill \frac{\text{opposite side}}{\text{hypotenuse}\hspace{0.5em},}\hfill & \hfill \hfill & \hfill \hfill \end{array}}$

and explained using the unit circle. Starting from this definition of $\sin (\alpha )$ we arrive at the sine function if we declare the angle $\alpha$ to be the independent variable of a function named $\sin$. This can be illustrated by means of a family of right triangles $ABC$ that are inscribed the unit circle, i.e. a circle with radius $r=1$, in a certain way.
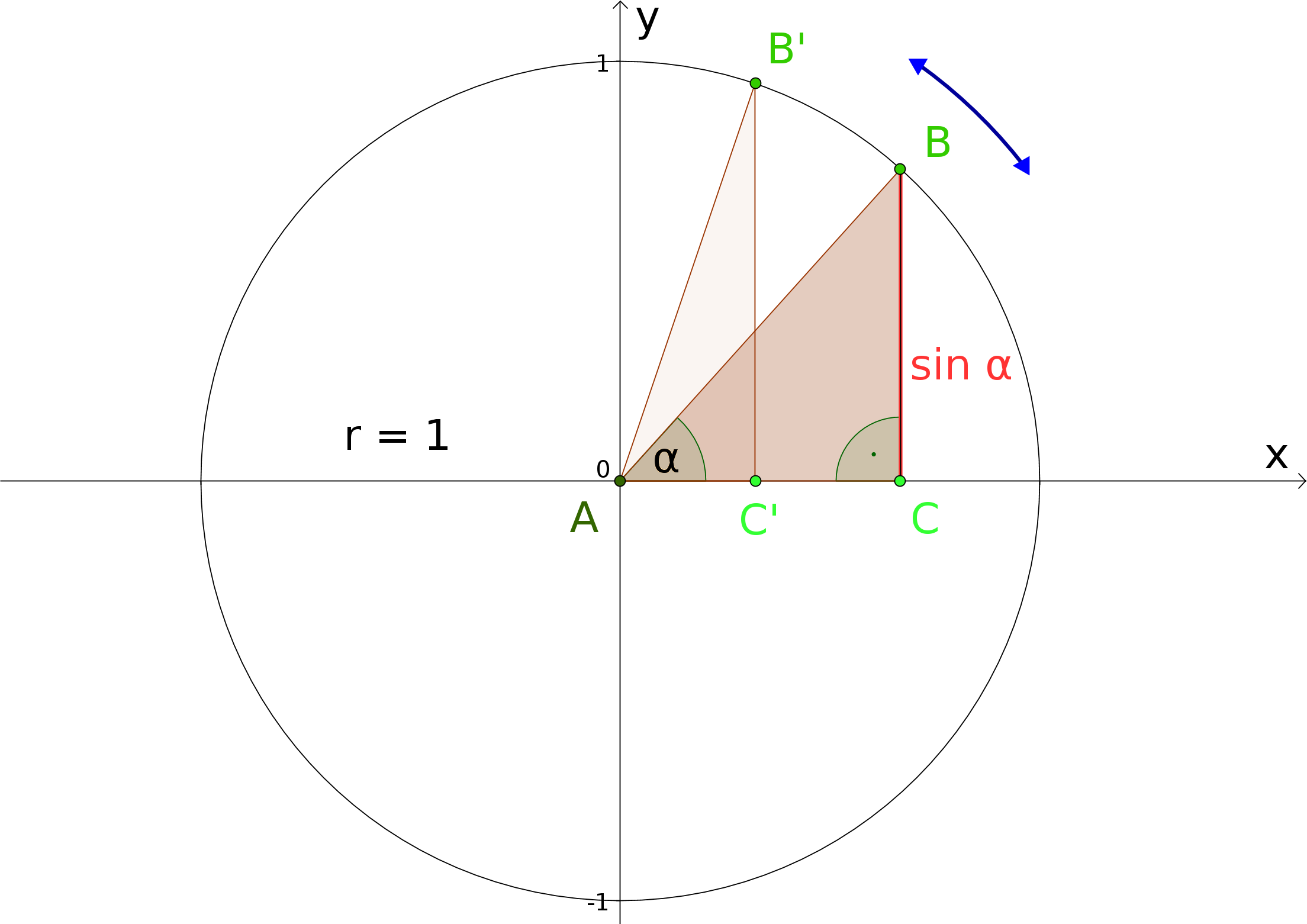
If we start with the angle $\alpha =0^{\circ }$, corresponding to a triangle degenerated to a line segment, then the length of the line segment $\overline{BC}$ equals $0$. If we now rotate the point $B$ counterclockwise around the circle, then the angle $\alpha$ - and $\sin (\alpha )$ as well - increases until for $\alpha ={90}^{\circ }$ a maximum value ($\sin ({90}^{\circ })=1$) is reached. Afterwards, the angle $\alpha$ continues to increase while $\sin (\alpha )$ is starting to decrease again. For $\alpha ={180}^{\circ }$, the triangle $ABC$ is again degenerated to a line segment and $\sin ({180}^{\circ })=0$. If $\alpha$ further increases, the triangle "flips downwards" and the line segment $\overline{BC}$ is oriented parallel to the negative vertical line ($y$-axis), hence, its length is negative. For $\alpha ={270}^{\circ }$ the maximum negative value occurs, before $\alpha$ approaches $0$ again. At $\alpha ={360}^{\circ }$ the game starts again. The figure above shows the graph of the sine function

${\displaystyle \sin :\mathrm{\hspace{0.5em}\hspace{0.5em}}\{\begin{array}{ccc}\hfill ℝ& \hfill \to \hfill & [-1;+1]\hfill \\ \hfill \alpha & \hfill ⟼\hfill & \sin (\alpha )\hfill \end{array}\hspace{0.5em}.}$


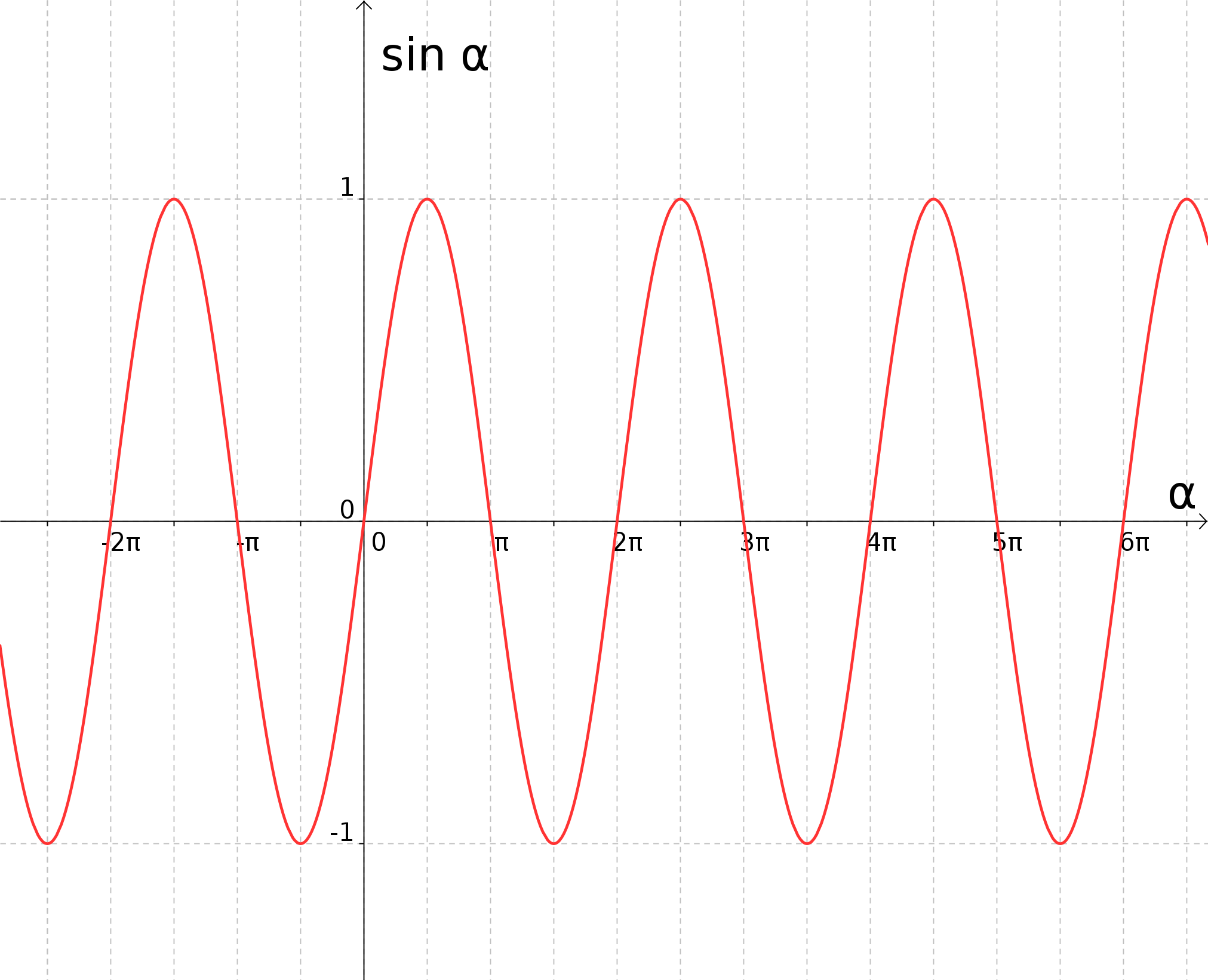
In contrast to the discussion so far, the angle $\alpha$ is plotted on the horizontal axis ($\alpha$-axis) in radian measure, used more commonly in this context, and not in degree measure.
Let us specify some of the most relevant properties of the sine function:

• The sine function is defined on the entire set of real numbers $ℝ$. Hence, $D_{\sin }=ℝ$. In contrast, the range only consists of the interval between $-1$ and $+1$, including these two endpoints: $W_{\sin }=[-1;+1]$.
  
• After certain measures, the graph of the since function repeats its shape exactly; in this context this is called the periodicity of the sine function. The period of the sine function is ${360}^{\circ }$ or $2\pi$. Mathematically, this relation can be expressed as
  
  ${\displaystyle \sin (\alpha )=\sin (\alpha +2\pi )\hspace{0.5em}.}$
  
  
  

Just a quick look at the graph of the simple sine function suggests that we could use this function for the description of wave phenomena. However, to be able to use the full potential of the sine function a few parameters will be introduced. For example, the amplitude of the sine function can be amplified or damped by a so-called amplitude factor $A$, the frequency of the oscillation can be affected by a frequency-like factor $a$, and the entire path of the graph can be shifted to the left or to the right by a shifting constant $b$. Thus, the general sine function has the following form:

${\displaystyle f:\mathrm{\hspace{0.5em}\hspace{0.5em}}\{\begin{array}{ccc}\hfill ℝ& \hfill \to \hfill & [-A;+A]\hfill \\ \hfill x& \hfill ⟼\hfill & f(x)=A\sin (\mathrm{ax}+b)\hfill \end{array}\hspace{0.5em}.}$