Chapter 6 Elementary Functions
Section 6.5 Trigonometric Functions6.5.3 Cosine and Tangent Function
Essentially, for the cosine function and the tangent function we have to do the same considerations as for the sine function that we already know from Subsection 6.5.2. As we have some experience, we can shorten the discussion a bit. We start with the cosine function and consider again our triangles inscribed the unit circle.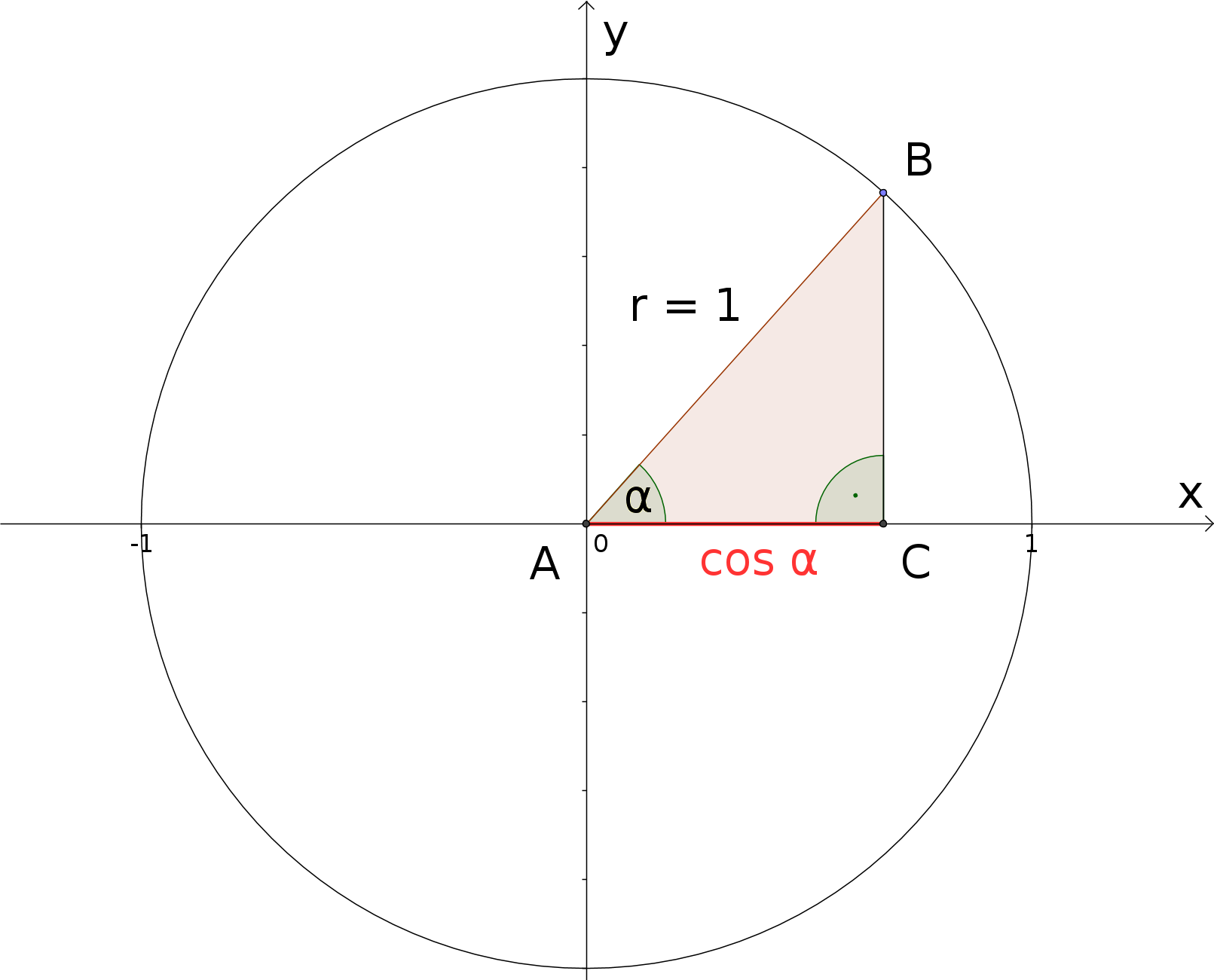
What are the relevant properties of the cosine function?
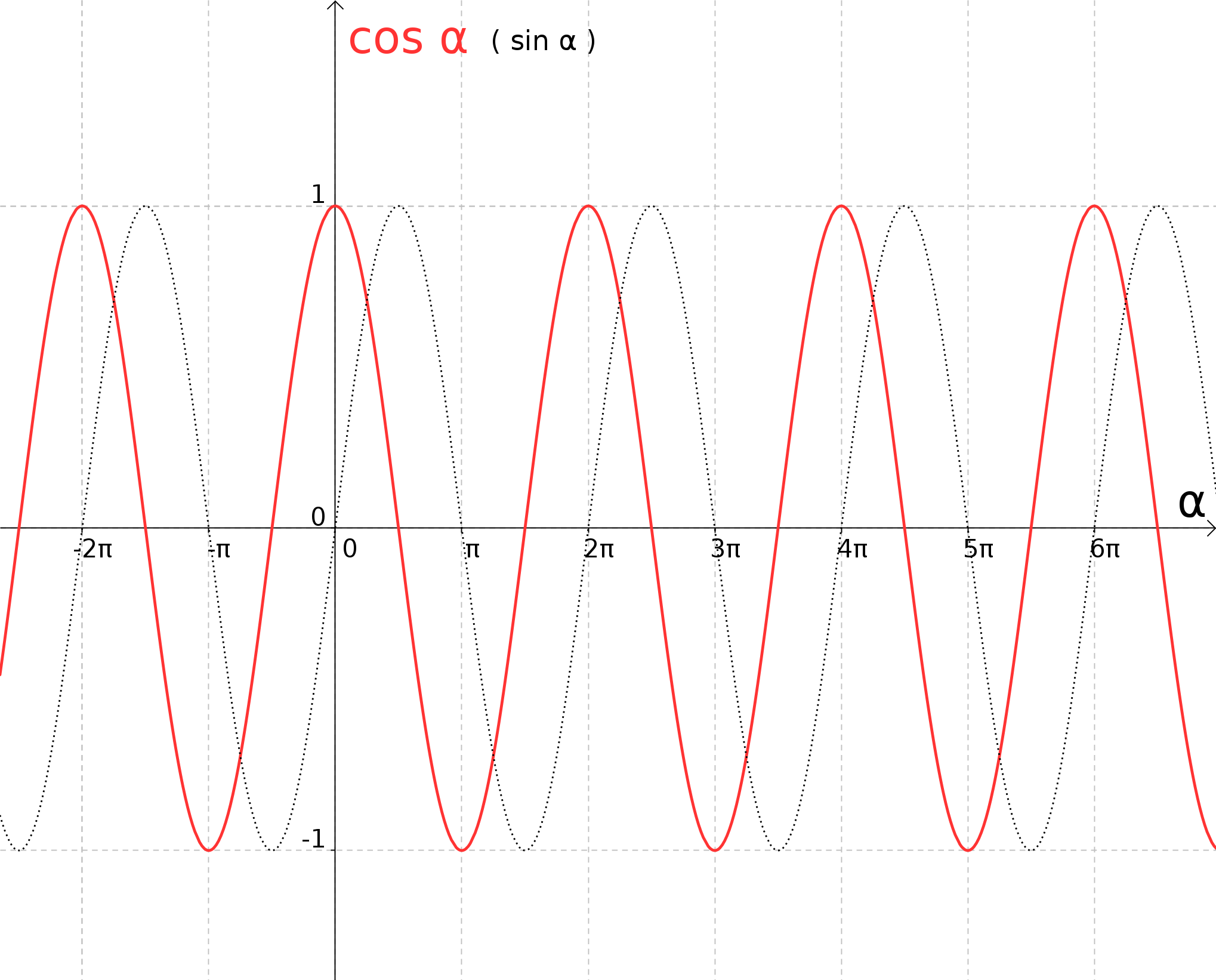
- The cosine function is also a periodic function. The period is again or .
- The domain of the cosine function consists of the entire set of the real numbers. Hence, . The range is the interval between and , including the endpoints: .
- From the figure above, showing and , we immediately see that
for all real values of . Also true, but not as obvious, is the relation
As in the case of the sine, the cosine has also a general cosine function. In its definition additional degrees of freedom occur in form of parameters (amplitude factor , frequency factor , and shifting constant ). In this way, it is possible to fit the function's graph to different situations (in application examples):
Exercise 6.5.3
In Example 6.5.1 we briefly discussed the simple pendulum. In particular, the displacement angle of the pendulum can be determined as a function of time under the condition that the period equals seconds and that the pendulum at is started with an initial displacement angle of :
Can this situation also be described using the (general) cosine function (instead of the sine function), and if so, what form does take in this case?
Can this situation also be described using the (general) cosine function (instead of the sine function), and if so, what form does take in this case?
The tangent is the ratio of sine to cosine: . Thus, it follows immediately that the tangent function cannot be defined for all real numbers since finally the cosine function has an infinite number of roots. This can be seen, for example, in Exercise 6.5.2. In Exercise 6.5.2 also the positions of the roots of the cosine function are determined, namely . Thus, the domain of the tangent function is .
And what about the range? At the roots of the cosine function the tangent function tends to infinite positive or negative values and has a pole, and at the root of the sine function the ratio of sine and cosine is zero. In between, all values can be taken by the tangent function, and hence . All in all, for the tangent function we have
The graph of the function is shown in the figure below.
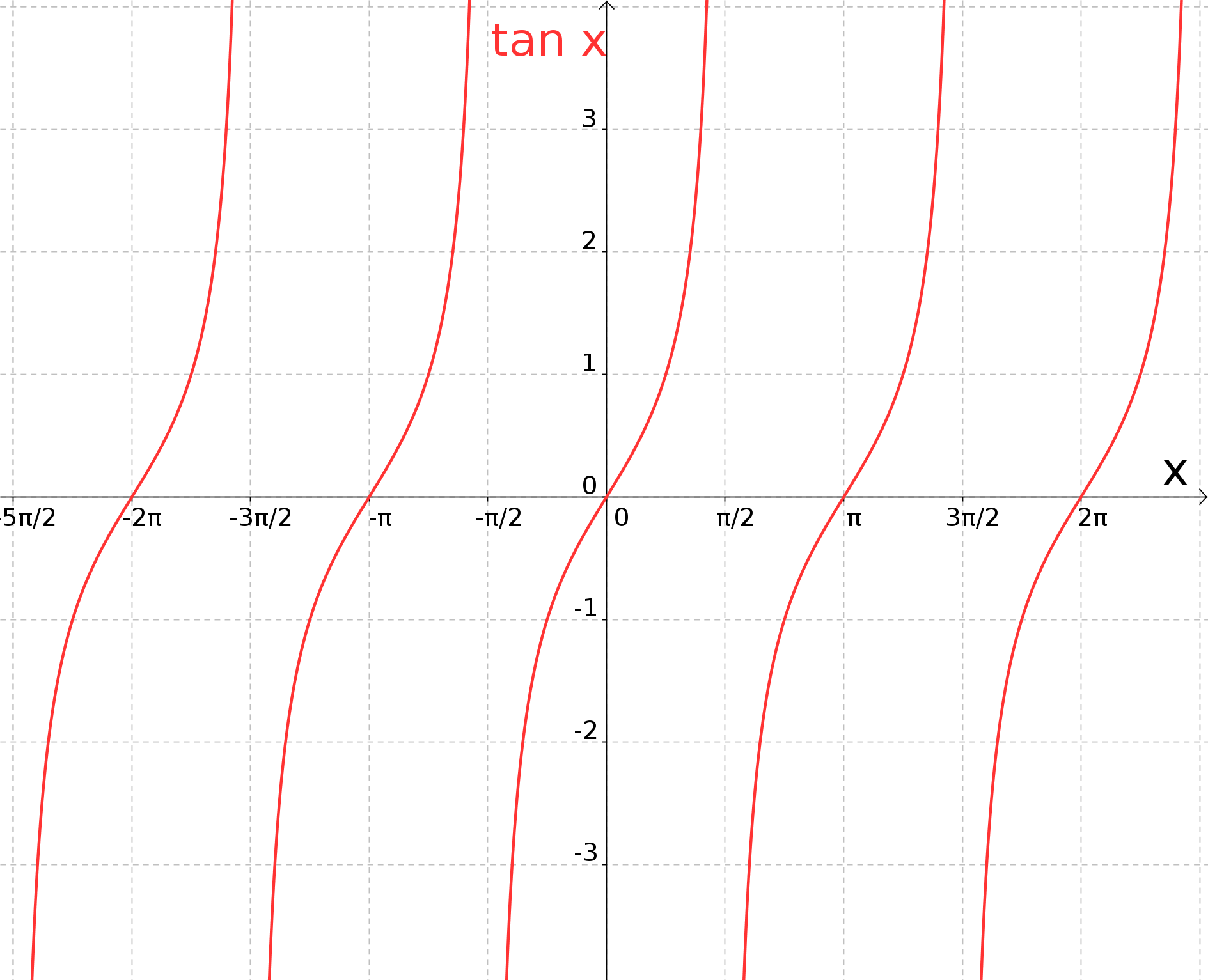
In addition, the tangent function is periodic, however, the period is or .
Exercise 6.5.4
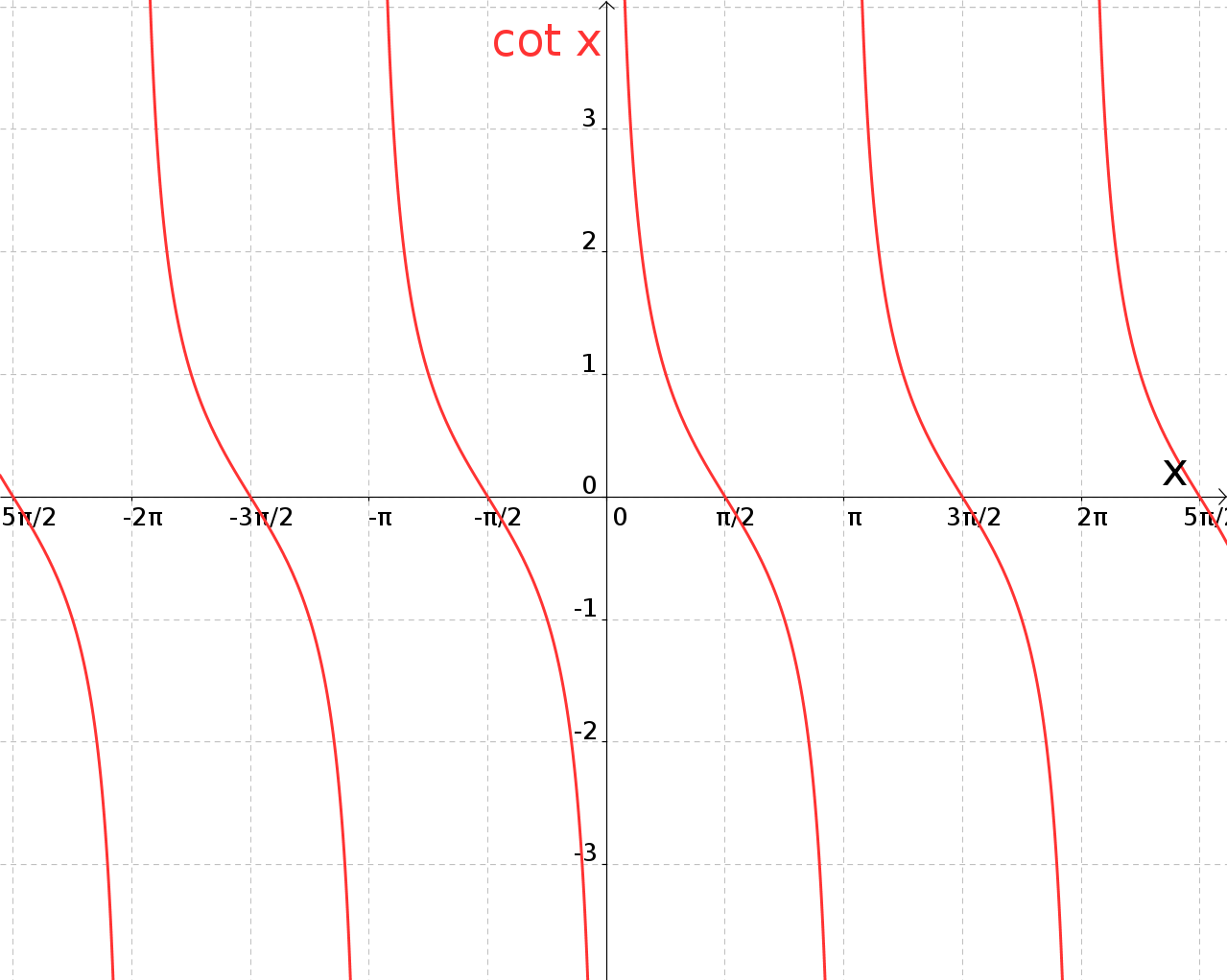
The so-called cotangent function (abbreviated to ) is defined by .
Specify the domain and the range of the cotangent function.
Specify the domain and the range of the cotangent function.
 Onlinebrückenkurs Mathematik
Onlinebrückenkurs Mathematik